\(\text{CauchyCDF}\)

You can use the \(\text{CauchyCDF}\) function to calculate the cumulative distribution function (CDF) of the Cauchy-Lorentz distribution.

You can use the \cauchyc backslash command to insert this function.

The following variants of this function are available:

• \(\text{real } \text{CauchyCDF} \left ( \text{<x>}, \text{<location>}, \text{<}\gamma\text{>} \right )\)

Where \(x\), \(location\), and \(\gamma\) are scalar values representing the value of interest, the location or offset, and the scale term respectively. Note that this function is defined over the range \(\gamma > 0\) and will generate a runtime error or return NaN for values for which the function is not defined.

The value is calculated directly using the relation:

\[\text{CauchyCDF} \left ( x, l, \gamma \right ) = \frac{1}{\pi} \text{arctan} \left ( \frac{x - l}{\gamma} \right ) + \frac{1}{2}\]

Figure 112 shows the basic use of the \(\text{CauchyCDF}\) function.

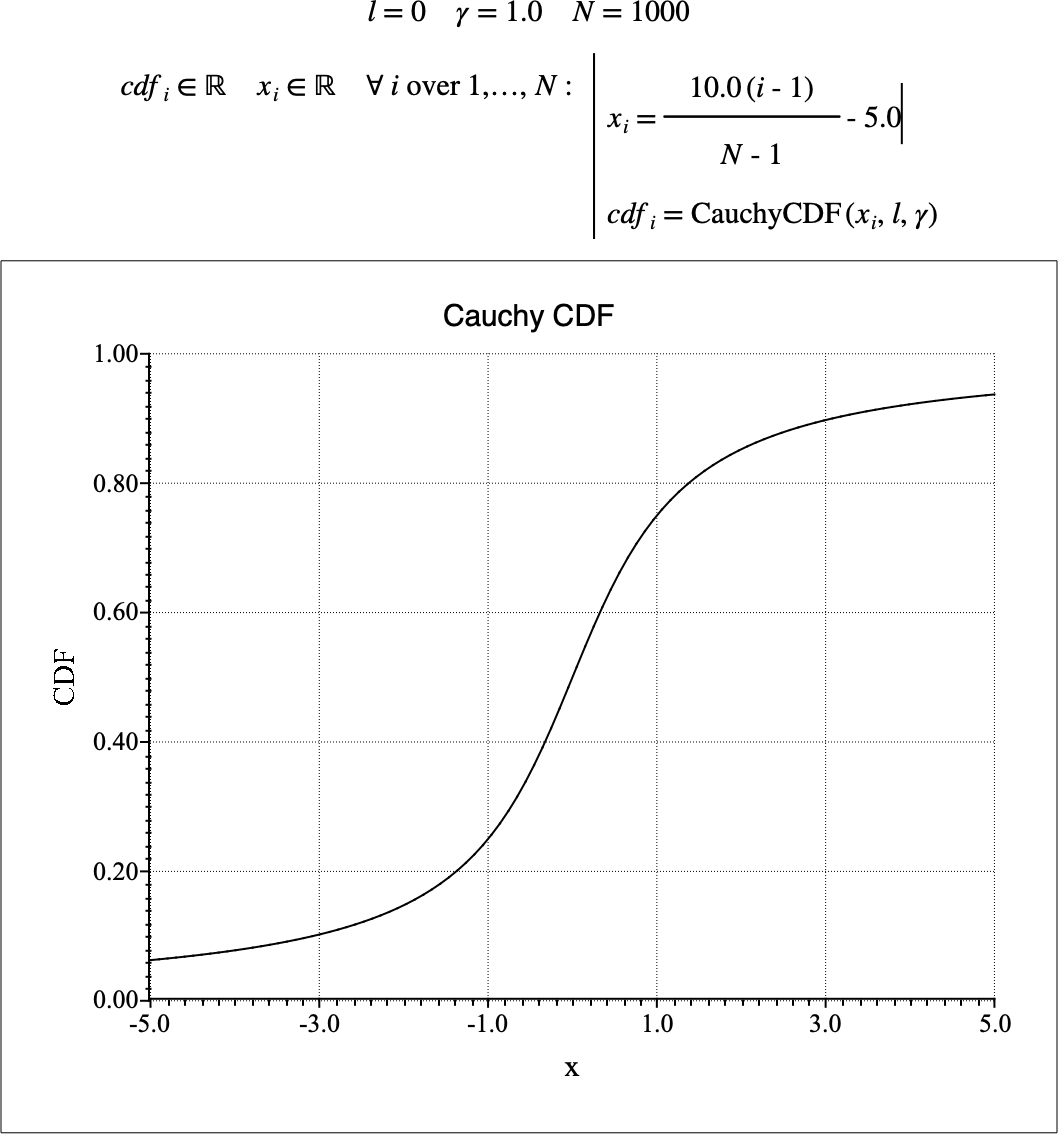
Figure 112 Example Use Of the CauchyCDF Function