\(\text{IsNormal}\)

You can use the \(\text{IsNormal}\) function to determine if a matrix is normal.

You can use the \isnormal backslash command to insert this function.

The following variants of this function are available:

• \(\text{boolean } \text{IsNormal} \left ( \text{<matrix>} \right )\)

• \(\text{boolean } \text{IsNormal} \left ( \text{<matrix>}, \text{<relative tolerance>} \right )\)

The \(\text{<matrix>}\) parameter is the matrix to be tested. The optional \(\text{<relative tolerance>}\) parameter specifies the tolerance to apply when comparing values. If not specified, the \(\text{IsNormal}\) function will use a tolerance of \(1.0 \times 10^{-8}\).

A matrix, \(M\), is considered normal if \(A^H A = A A^H\). The \(\text{isNormal}\) function relaxes this constraint by performing the test within a given tolerance. The \(\text{IsNormal}\) function considers a matrix to be normal if the matrix, \(M\), is square and:

\[M _ 1 = A^H A \;\;\;\;\; M _ 2 = A A^H\]

\[\left \vert M _ { 1,i,j } - M _ { 2,i,j } \right \vert \leq \frac{1}{2} \left \vert M _ { 1,i,j } + M _ { 2,i,j } \right \vert t _ {rel}\]

For all \(1 \leq i \leq \text{nrows} \left ( M \right )\) and \(1 \leq j \leq \text{ncols} \left ( M \right )\) where \(t _ {rel}\) is the relative tolerance. Note that this test is only applied if \(M _ { 1,i,j } \ne M _ { 2,i,j }\).

Figure 162 shows the basic use of the \(\text{IsNormal}\) function.

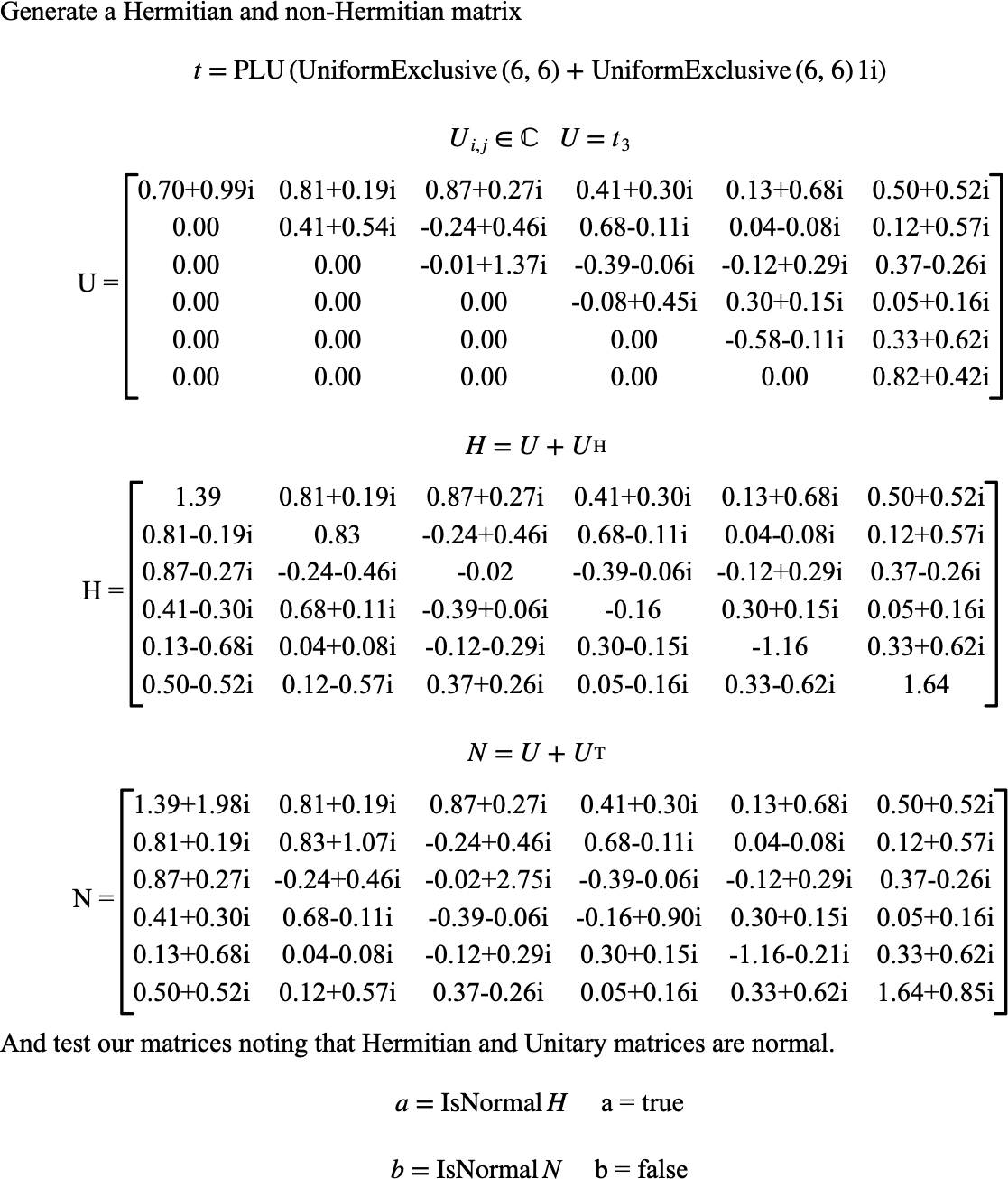
Figure 162 Example Use Of The IsNormal Function