\(\text{NormalVariate}\)¶
You can use the \(\text{NormalVariate}\) function to calculate one or more random variates in a normal or Gaussian distribution.
You can use the \normalv backslash command to insert this function.
The following variants of this function are available:
\(\text{real } \text{NormalVariate} \left ( \text{<}\mu\text{>} \right )\)
\(\text{real } \text{NormalVariate} \left ( \text{<}\mu\text{>}, \text{<}\sigma\text{>} \right )\)
\(\text{real matrix } \text{NormalVariate} \left ( \text{<number rows>}, \text{<number columns>}, \text{<}\mu\text{>} \right )\)
\(\text{real matrix } \text{NormalVariate} \left ( \text{<number rows>}, \text{<number columns>}, \text{<}\mu\text{>}, \text{<}\sigma\text{>} \right )\)
The \(\text{<}\mu\text{>}\), and \(\text{<}\sigma\text{>}\) are scalar
values representing the mean value of the distribution, and the standard
deviation respectively. The \(\text{<}\sigma\text{>}\) parameter is
optional, if not specified, a value of 1 is used. Note that the function is
defined over the range \(\sigma > 0\) and will generate a run-time error or
return NaN or a matrix of NaN for values for which the function is not
defined.
The one and two parameter versions return a single value. The three and four parameter version return a matrix of real values.
The \(\text{NormalVariate}\) uses Marsaglia’s polar method [5] to calculate random variates in a normal distribution. The matrix version of the \(\text{NormalVariate}\) function has been optimized to rapidly produce a large number of simultaneous normal random variates.
The normal distribution is one of the most widely used distribution as it represents the sum of a large number of random processes with fininte mean and variance. The resulting distribution from the sum will approach the normal distribution as the number of random processes approaches infinity. In practice, only a small number of random processes are needed to obtain a close approximation of the normal distribution.
Figure 183 shows the basic use of the \(\text{NormalVariate}\) function.
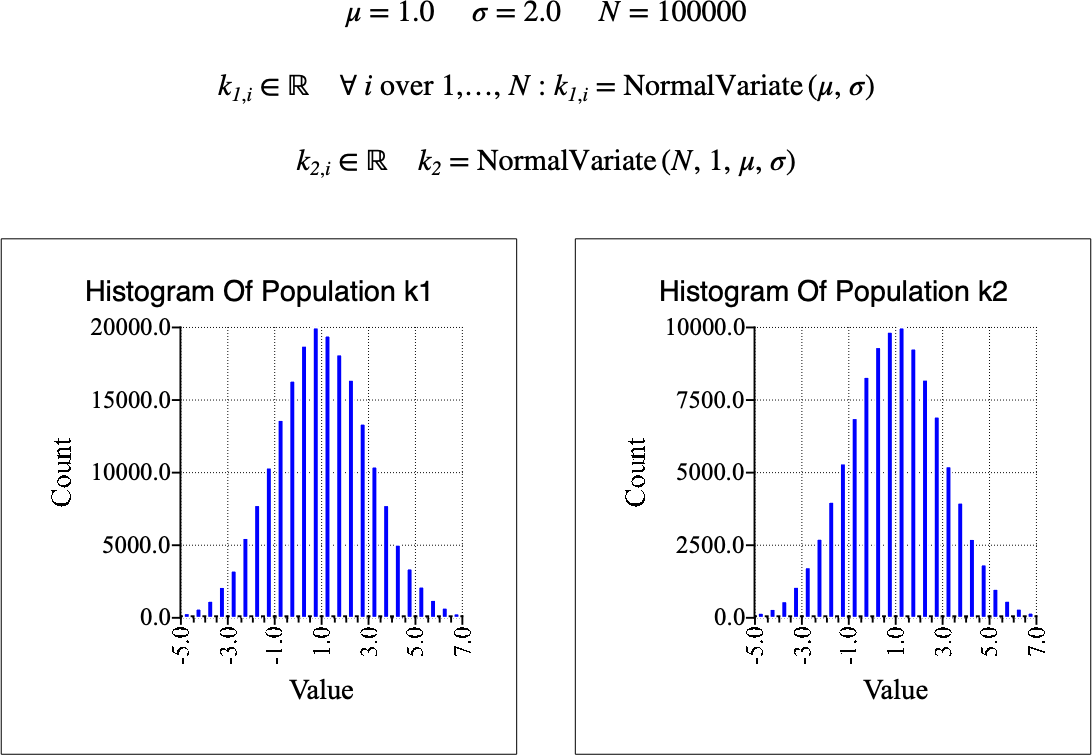
Figure 183 Example Use Of The NormalVariate Function¶
