\(\text{pNorm}\)

You can use the \(\text{pNorm}\) function to calculate the entry-wise p-norm of a matrix defined by:

\[\left \Vert X \right \Vert _ p = \sqrt[p]{ \sum_{r=1}^{nrows \left ( X \right ) } \sum_{c=1}^{ncols \left ( X \right ) } \left \vert X _ { r,c } \right \vert ^ p }\]

You can use the \pnorm backslash command to insert this function.

The following variants of this function are available:

• \(\text{real } \text{pNorm} \left ( \text{<matrix>}, \text{<p>} \right )\)

Where \(\text{<matrix>}\) can be any matrix type and \(\text{<p>}\) represents the type of entry-wise norm to be calculated. The function is defined for

The function is implemented internally for real and complex matrices. Other matrix types will be converted to real matrices prior to calculating the norm.

Figure 186 shows the basic use of the \(\text{pNorm}\) function.

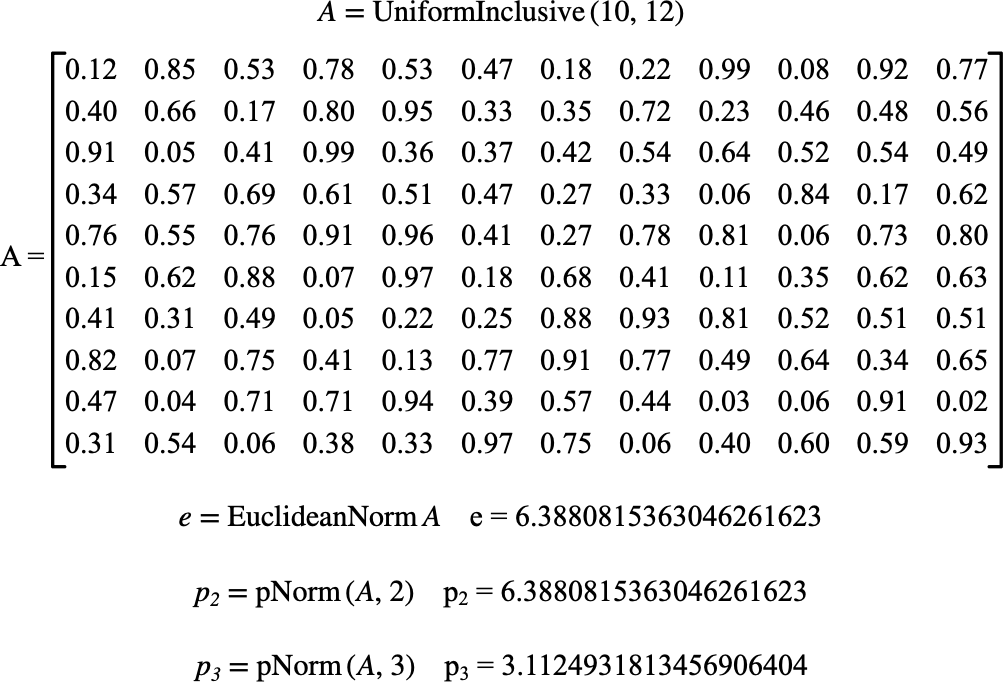
Figure 186 Example Use Of The pNorm Function