\(\text{RayleighVariate}\)

You can use the \(\text{RayleighVariate}\) function to calculate one or more random variates in a Rayleigh distribution.

You can use the \rayleighv backslash command to insert this function.

The following variants of this function are available:

• \(\text{real } \text{RayleighVariate} \left ( \text{<}\sigma\text{>} \right )\)

• \(\text{real matrix } \text{RayleighVariate} \left ( \text{<number rows>}, \text{<number columns>}, \text{<}\sigma\text{>} \right )\)

Where \(\sigma\) is a scalar values the scale term. Note that this funciton is defined over the range \(\sigma > 0\) and will generate a runtime error, return NaN, or return a matrix of NaN for values for which the function is not defined.

The single parameter version returns a single random variate. The three parameter version returns a real matrix of random variates.

The \(\text{RayleighVariate}\) calculate random variates by transformation method using the function:

\[\text{RayleighVariate} \left ( \sigma \right ) = \sigma \sqrt{-2 \ln \left ( u \right )}\]

Where \(u\) is a uniform random variage over the range (0, 1). The matrix version is optimized to calculate random variates in bulk and uses SIMD instructions to perform the transformation on multiple values simultaneously.

Figure 195 shows the basic use of the \(\text{RayleighVariate}\) function.

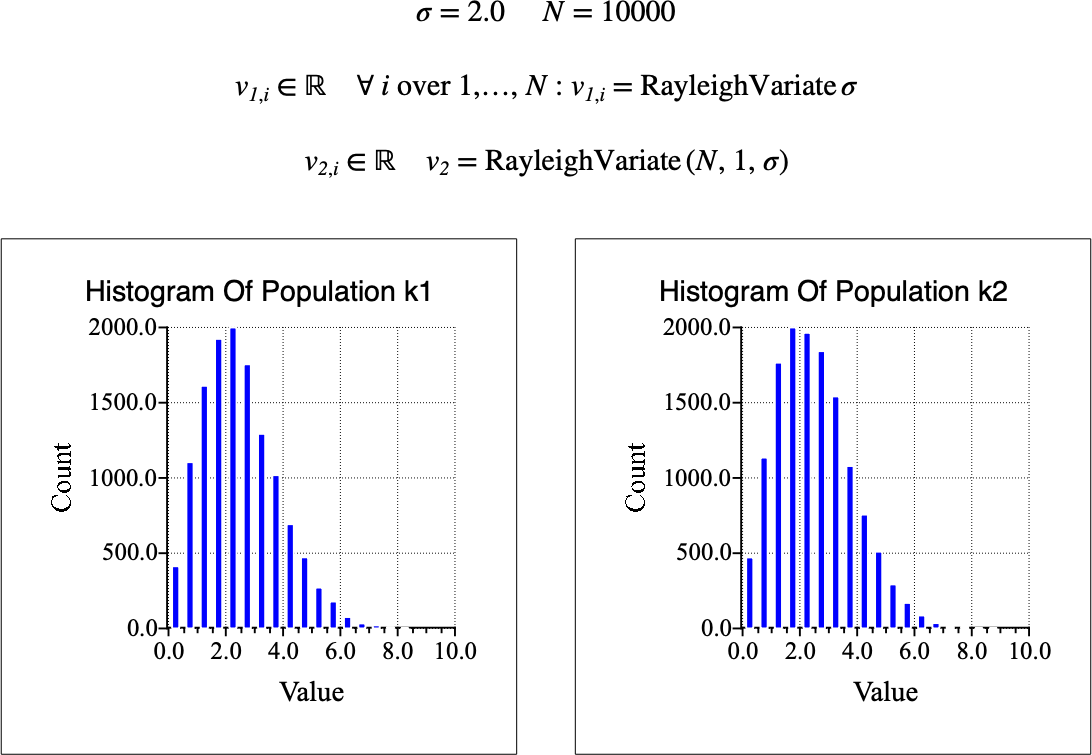
Figure 195 Example Use Of the RayleighVariate Function