\(\text{SVD}\)

You can use the \(\text{SVD}\) function to perform a singular value decomposition (SVD) of a matrix.

You can use the \svd backslash command to insert this function.

The following variants of this function are available:

• \(\text{tuple } \text{SVD} \left ( \text{<matrix>} \right )\)

The \(\text{<matrix>}\) parameter is the matrix to calculate the singular value decomposition of. The \(\text{SVD}\) function returns a tuple containing:

• The \(U\) unitary matrix.

• The \(\Sigma\) real diagonal matrix.

• The \(V\) unitary matrix.

• A boolean value indicating true on success or false on error.

The function is implemented internally for real and complex matrices although you can supply boolean and integer matrices which will be converted to real matrices prior to performing the singular value decomposition operation.

The singular value decomposition calculates a unitary matrix, \(U\) representing a rotation operation, a diagonal matrix, \(\Sigma\), representing a scaling operation, followed by a second unitary matrix, \(V\) representing a second rotation matrix. The original matrix can be reconstructed by:

\[M = U \Sigma V\]

Figure 211 shows the basic use of the \(\text{SVD}\) function.

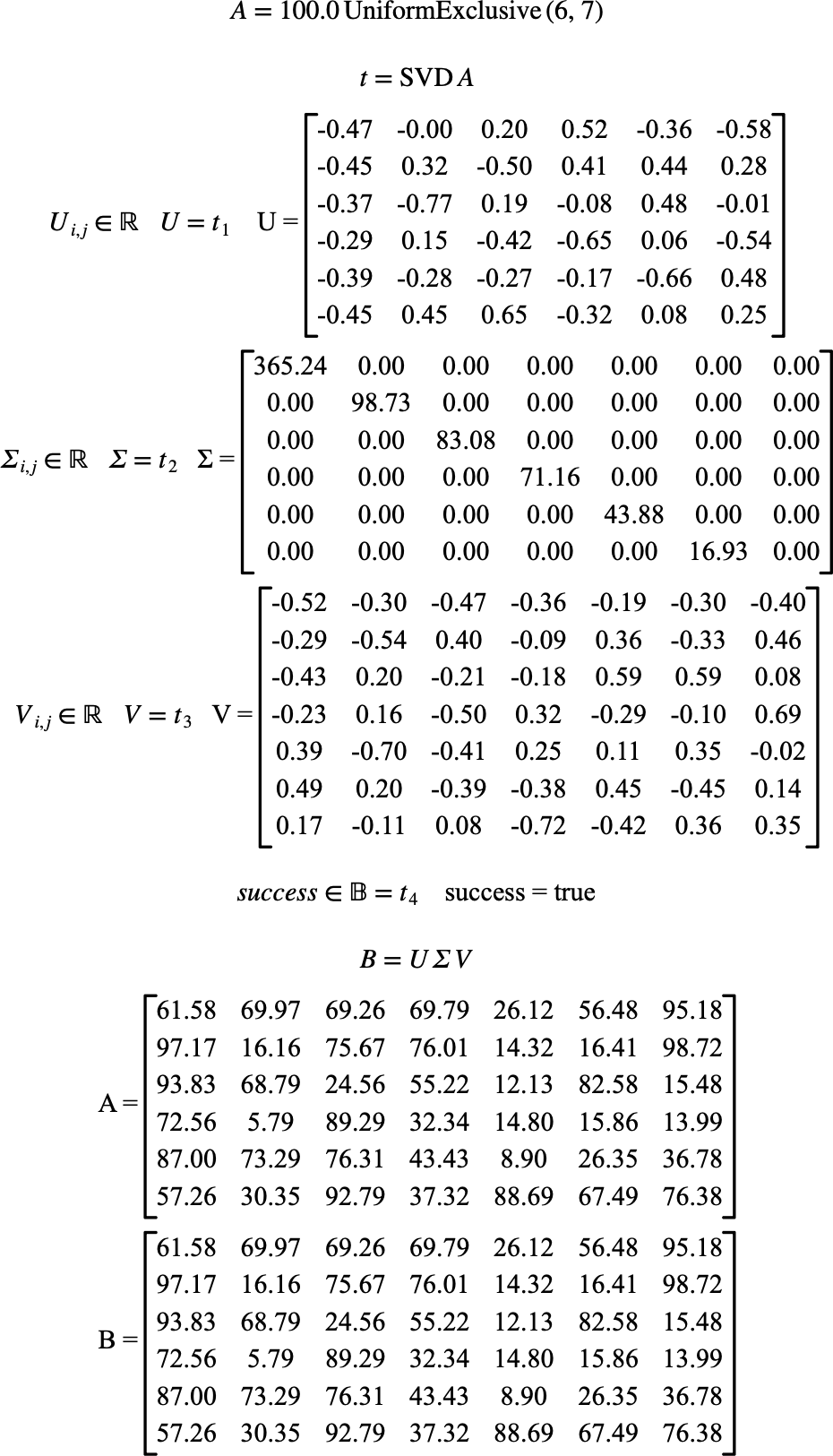
Figure 211 Example Use Of The SVD Function