\(\text{WeibullCDF}\)¶
You can use the \(\text{WeibullCDF}\) function to calculate the cumulative distribution function (CDF) of the Weibull distribution.
You can use the \weibullc backslash command to insert this function.
The following variants of this function are available:
\(\text{real } \text{WeibullCDF} \left ( \text{<x>}, \text{<k>}, \text{<}\lambda\text{>} \right )\)
\(\text{real } \text{WeibullCDF} \left ( \text{<x>}, \text{<k>}, \text{<}\lambda\text{>}, \text{<delay>} \right )\)
Where \(\text{<x>}\), \(\text{<k>}\), and
\(\text{<}\lambda\text{>}\) are scalar values representing the value of
interest, the shape term, and the scale term respectively. The
\(\text{WeibullCDF}\) function is defined over the range \(k > 0\) and
\(\lambda > 0\) and will generate an error or return NaN for values for
which the function is not defined.
The \(\text{<delay>}\) term is optional. If not specified, a delay of 0 is used.
The value is calculated directly using the relation:
Figure 219 shows the basic use of the \(\text{WeibullCDF}\) function.
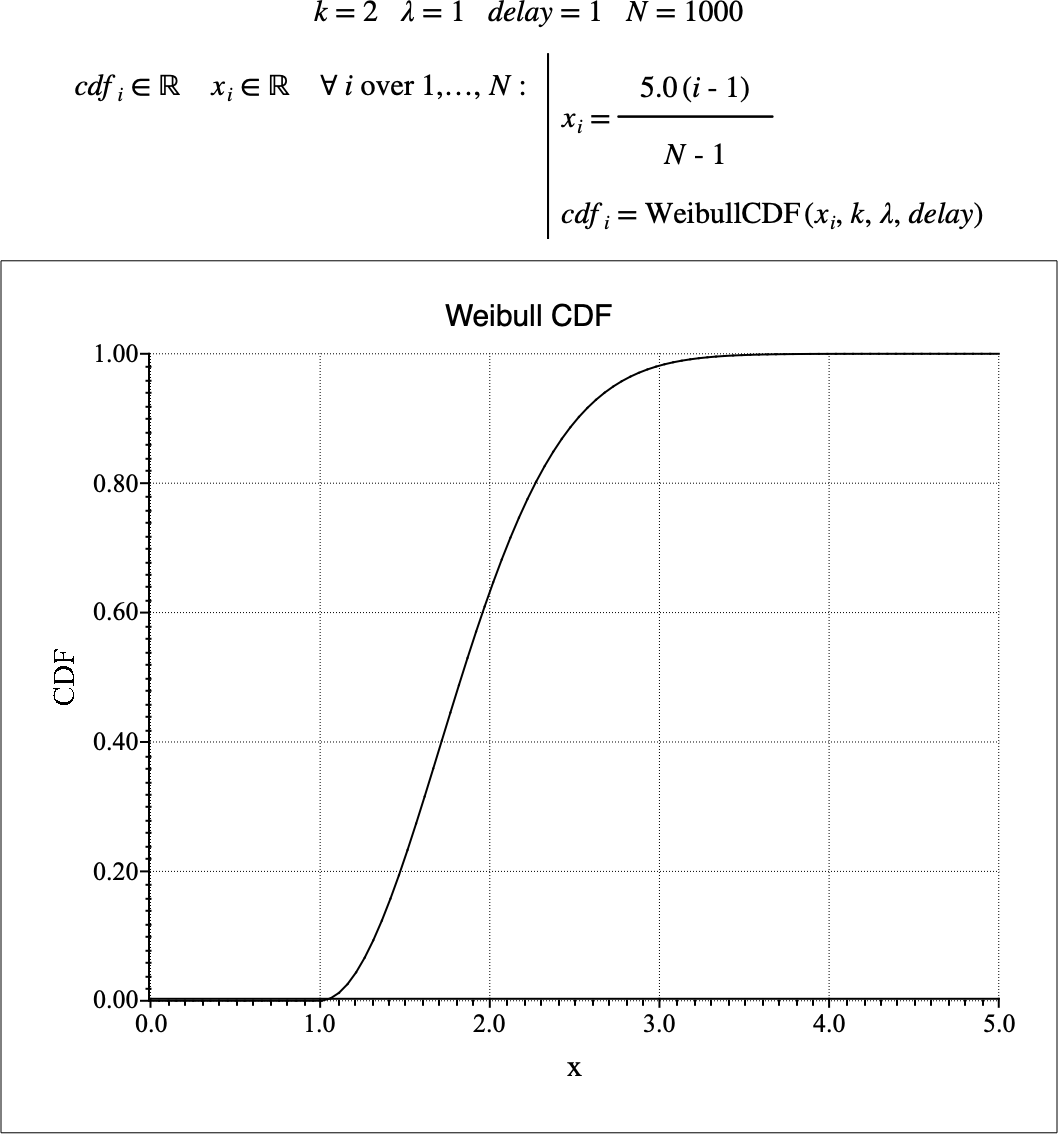
Figure 219 Example Use Of the WeibullCDF Function¶
