\(\text{BinomialPMF}\)

You can use the \(\text{BinomialPMF}\) function to calculate the probability mass function (PMF) of the binomial distribution.

You can use the \binomialp backslash command to insert this function.

The following variants of this function are available:

• \(\text{real } \text{BinomialPMF} \left ( \text{<k>}, \text{<n>}, \text{<p>} \right )\)

Where \(k\), \(n\), and \(p\) are scalar values. Note that this function is defined over the range \(k \geq 0\), \(n \geq 0\), and \(0 \leq p \leq 1\) and will either generate a run-time error or return NaN for all other values.

The returned value is calculated by:

\[\text{BinomialPMF} \left ( k, n, p \right ) = e ^ { \left [ \ln \binom{n}{k} + k \ln \left ( p \right ) + \left ( n - k \right ) \ln \left ( 1 - p \right ) \right ] }\]

Where \(\ln{\binom{n}{k}}\), the log-binomial function, is calculated directy rather than as the log of the binomial.

The binomial distribution can be used to determine the probability of \(k\) successes in \(n\) trials of an experiment where each trial has an independent probability of success \(p\). The distribution also assumes that each trial does not result in the reduction of the size of the sample population.

Example applications of the binomial distribution may include.

• Determining the probability of drawing \(k\) cards of a specific suit after \(n\) trials where cards are returned and the deck is shuffled after each trial.

• Determining the approximate probability of grabbing \(k\) black marbles from a handful of \(n\) marbles after blindly reaching into large bin where black marbles make of \(p\) fraction of the total population.

Figure 110 shows the basic use of the \(\text{BinomialPMF}\) function.

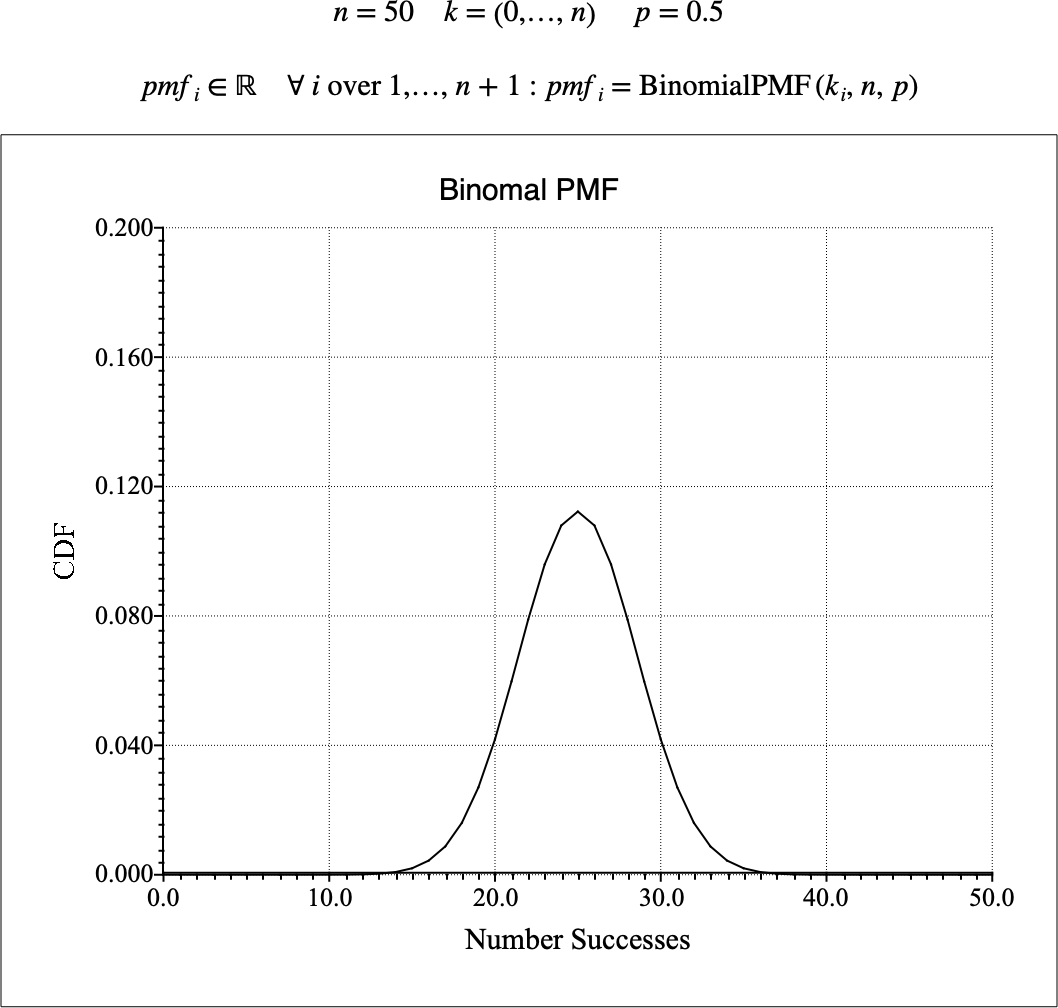
Figure 110 Example Use Of The BinomialPMF Function