\(\text{ChiSquaredPDF}\)

You can use the \(\text{ChiSquaredPDF}\) function to calculate the probability density function (PDF) of the chi-squared distribution.

You can use the \chisquaredp backslash command to insert this function.

The following variants of this function are available:

• \(\text{real } \text{ChiSquaredPDF} \left ( \text{<x>}, \text{<k>} \right )\)

Where \(x\) and \(k\) are scalar values indicating the value of interest and the degrees of freedom respectively. The function is defined for all \(k \in \mathbb{Z}\) where \(k > 0\) and where \(0 < x\) if \(k = 1\) and \(0 \leq x\) for all other values of \(k\).

The value is calculated directly using the relation:

\[\text{ChiSquaredPDF} \left ( x, k \right ) = \frac{1} {2 ^ {\frac{k}{2}} \Gamma \left ( \frac{k}{2} \right )} x ^ { \frac{k}{2} - 1 } e ^ {- \frac{x}{2}}\]

The chi-squared distribution represents the sum of the squares of \(k\) standard normally distributed random variates.

Figure 117 shows the basic use of the \(\text{ChiSquaredPDF}\) function.

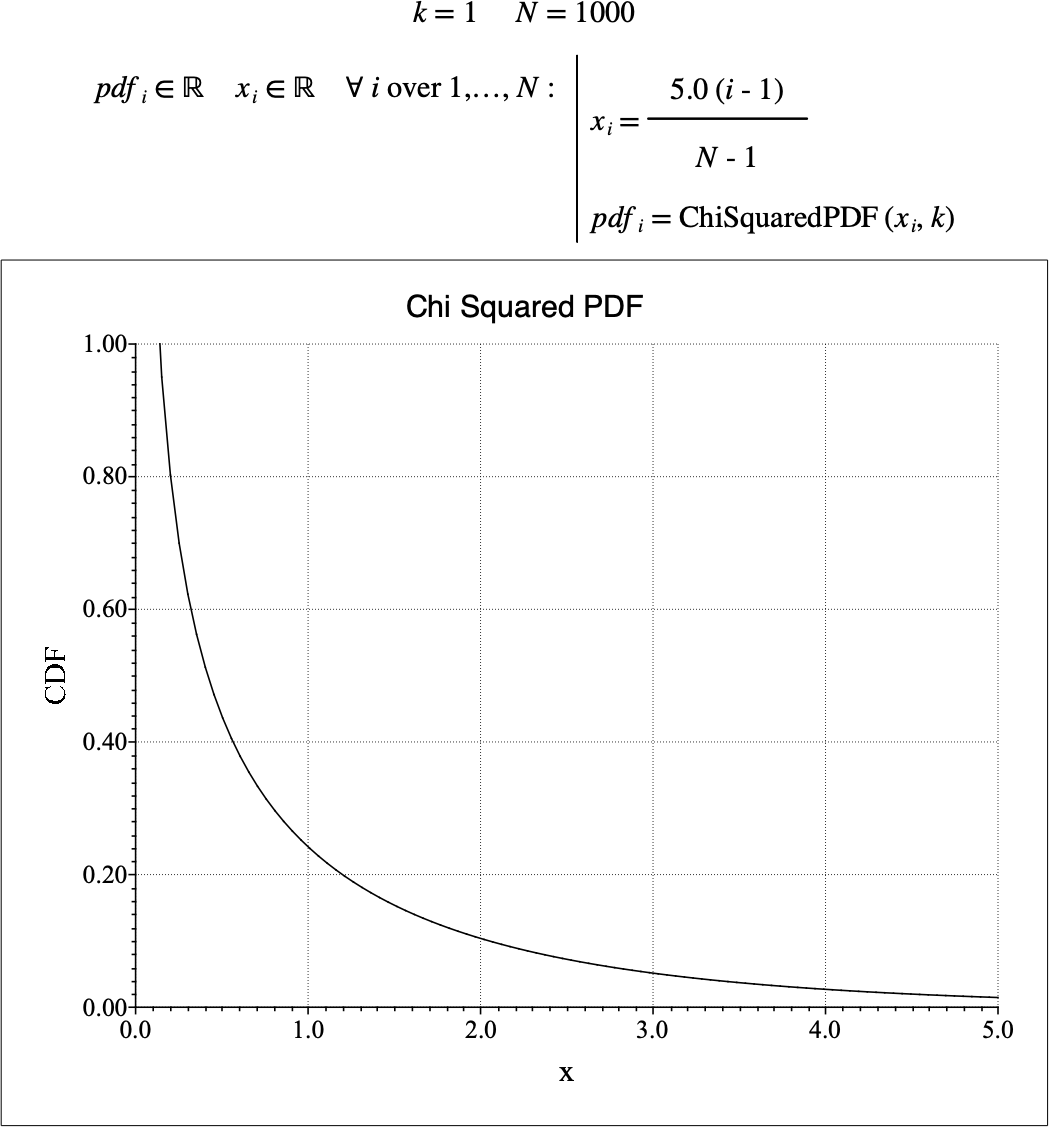
Figure 117 Example Use Of the ChiSquaredPDF Function