\(\text{ChiSquaredQuantile}\)¶
You can use the \(\text{ChiSquaredQuantile}\) function to calculate the quantile function of the chi-squared distribution. The quantile function is the inverse of the cumulative distribution function.
You can use the \chisquaredq backslash command to insert this function.
The following variants of this function are available:
\(\text{real } \text{ChiSquaredQuantile} \left ( \text{<p>}, \text{<k>} \right )\)
Where \(x\) and \(k\) are scalar values indicating the value of interest and the degrees of freedom respectively. The function is defined for all \(k \in \mathbb{Z}\) where \(k > 0\) and where \(0 < x\) if \(k = 1\) and \(0 \leq x\) for all other values of \(k\).
The value is calculated directly using the relation:
Where \(\gamma\text{Inv}\) is the inverse lower gamma function. evaluated for the second term.
The chi-squared distribution represents the sum of the squares of \(k\) standard normally distributed random variates.
Figure 118 shows the basic use of the \(\text{ChiSquaredQuantile}\) function.
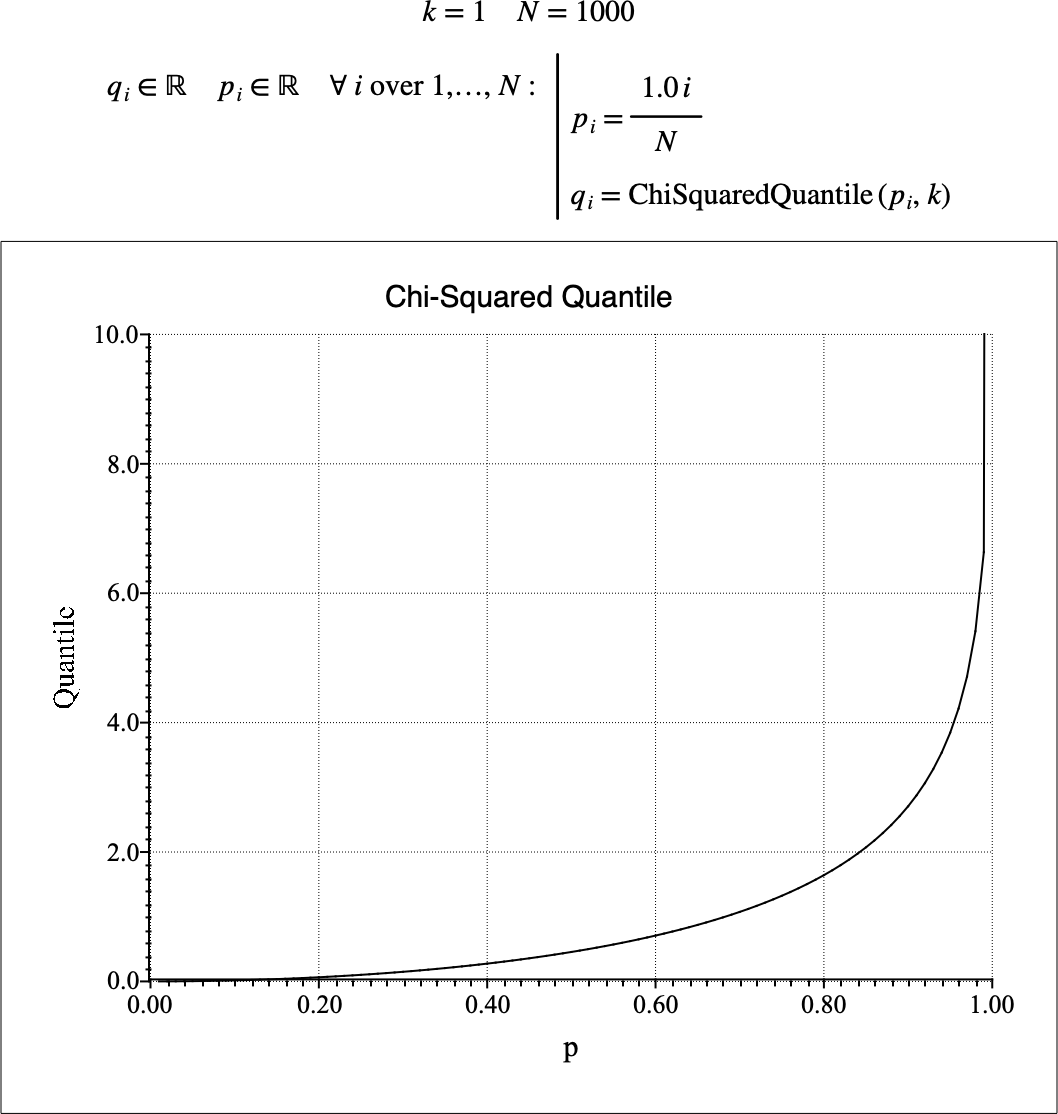
Figure 118 Example Use Of the ChiSquaredQuantile Function¶
