\(\text{ExponentialVariate}\)

You can use the \(\text{ExponentialVariate}\) function to calculate one or more random variates in an exponential distribution.

You can use the \exponentialv backslash command to insert this function.

The following variants of this function are available:

• \(\text{real } \text{ExponentialVariate} \left ( \text{<}\lambda\text{>} \right )\)

• \(\text{real matrix } \text{ExponentialVariate} \left ( \text{<number rows>}, \text{<number columns>}, \text{<}\lambda\text{>} \right )\)

Where \(\lambda\) is a scalar value representing the desired rate. Note that this function is defined over the range \(\lambda > 0\) and will generate a runtime error, return NaN or a matrix of NaN for values where the distribution is not defined.

The three parameter version, which includes \(\text{<number rows>}\) and \(\text{<number columns>}\) fields, returns an real matrix returning random deviates. The single parameter version returns a single value.

This function calculates random variates using transformation method based on definition of the quantile function:

\[\text{ExponentialVariate} \left ( \lambda \right ) = - \frac{\ln \left ( u \right )} {\lambda}\]

where \(u\) is a random variate over a uniform distribution over the range \(0 < u < 1\). The matrix version uses the same algorithm but has been optimized to compute values using SIMD instructions for improved performance.

The exponential distribution, along with the geometric distribution, has the property that the probability of an event occuring over some interval is independent of the start time of that interval.

\[Pr \left ( T \leq t _ 1 | T \geq t _ 0 \right ) = Pr \left ( 0 \leq T \leq t _ 1 - t _ 0 \right )\]

Where \(0 \leq t _ 0 \leq t _ 1\).

The exponential distribution is often used to model traffic from uncorrelated sources, such as arrival of cars at an intersection or customers into a queue. The exponential distribution is a special case of both the gamma distribution and the Erlang distribution.

The exponential distribution is also often used to model failure rate and is a special case of Weibull distribution.

Figure 133 shows the basic use of the \(\text{ExponentialVariate}\) function.

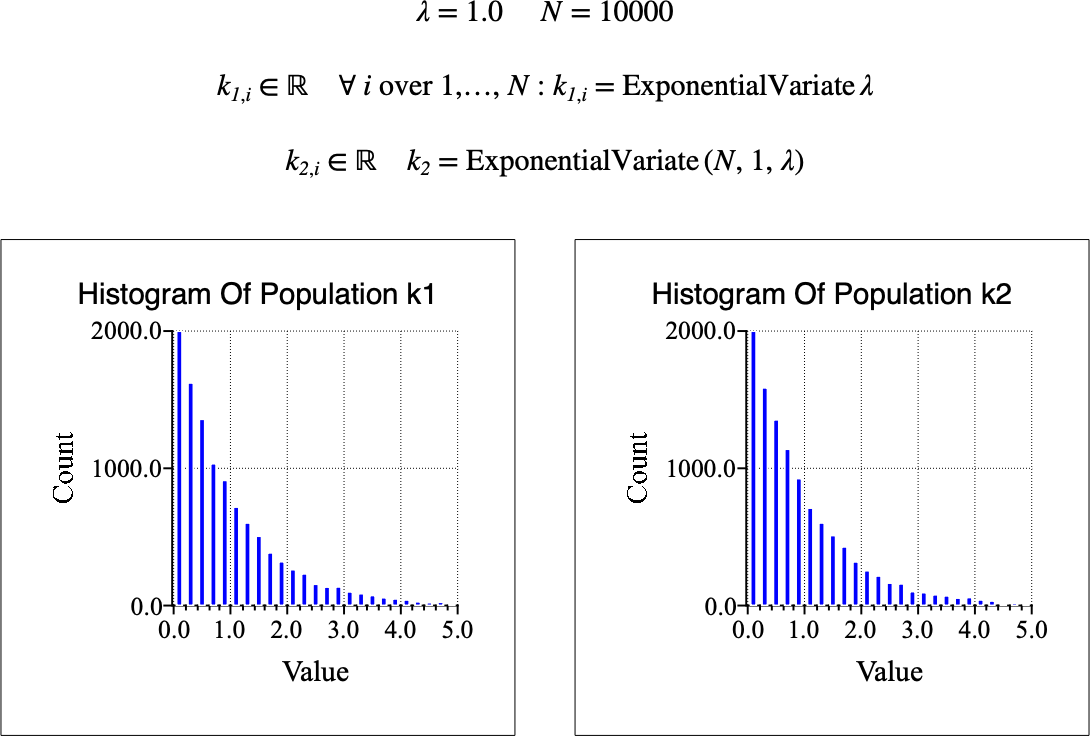
Figure 133 Example Use Of the ExponentialVariate Function

Note that you can also use this function to calculate random variates in a Laplace distribution as shown in Figure 134.

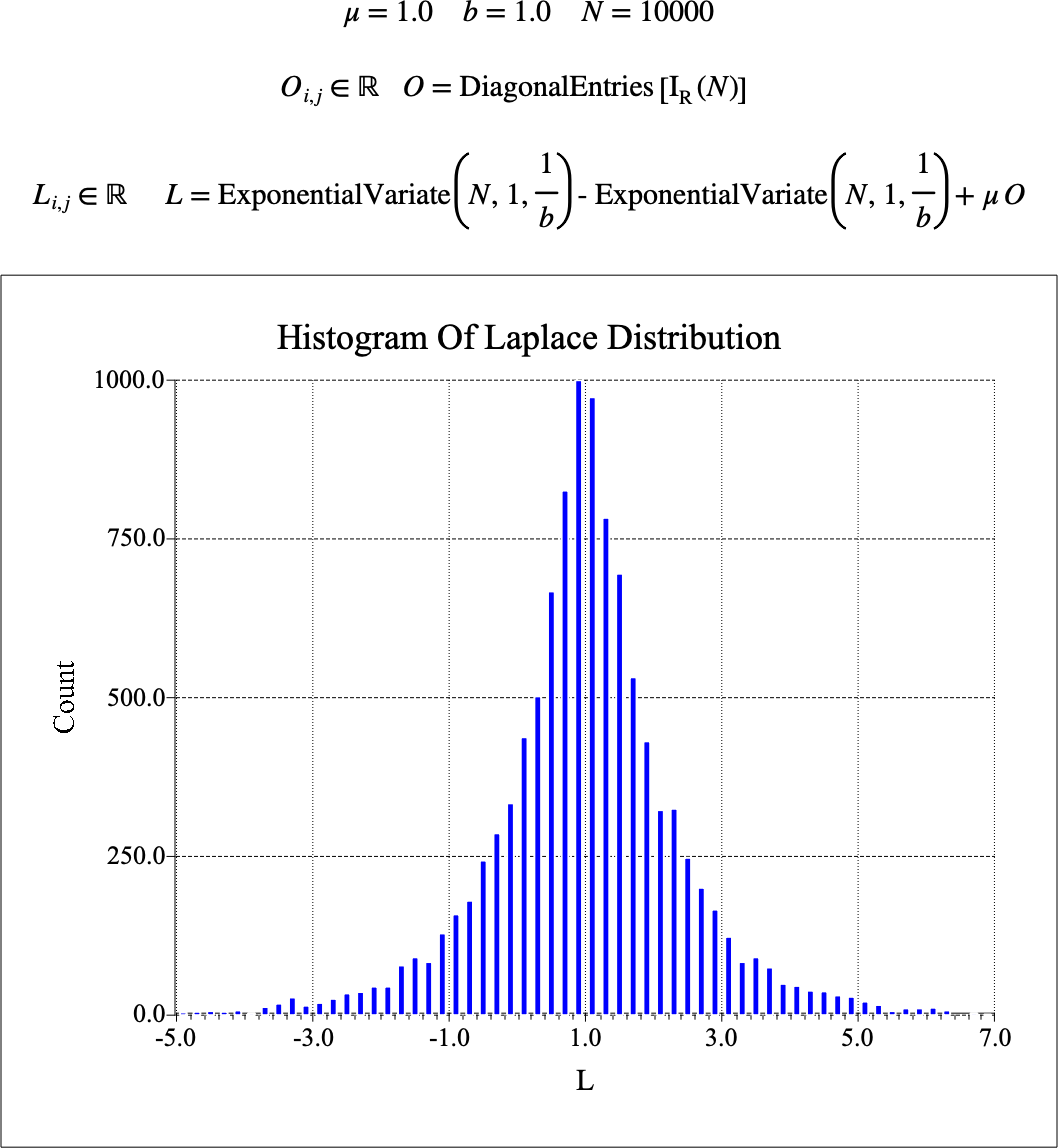
Figure 134 Generating Random Variates In A Laplace Distribution