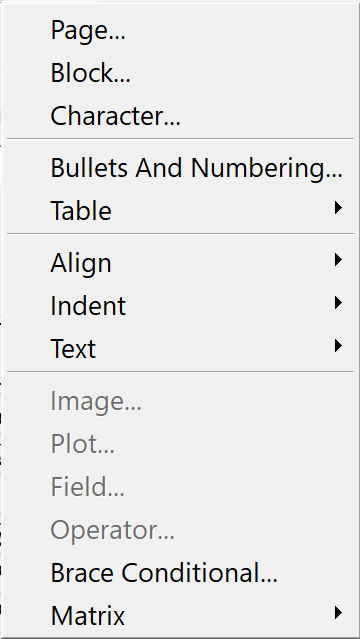
Documenting Your Algorithm¶
This section explains how to use the Aion user interface to simultaneously create and document your algorithm.
Main Window¶
Figure 2, Figure 3, and Figure 4 shows the Aion main window on Microsoft Windows, Apple MacOS, and Linux using KDE respectively.
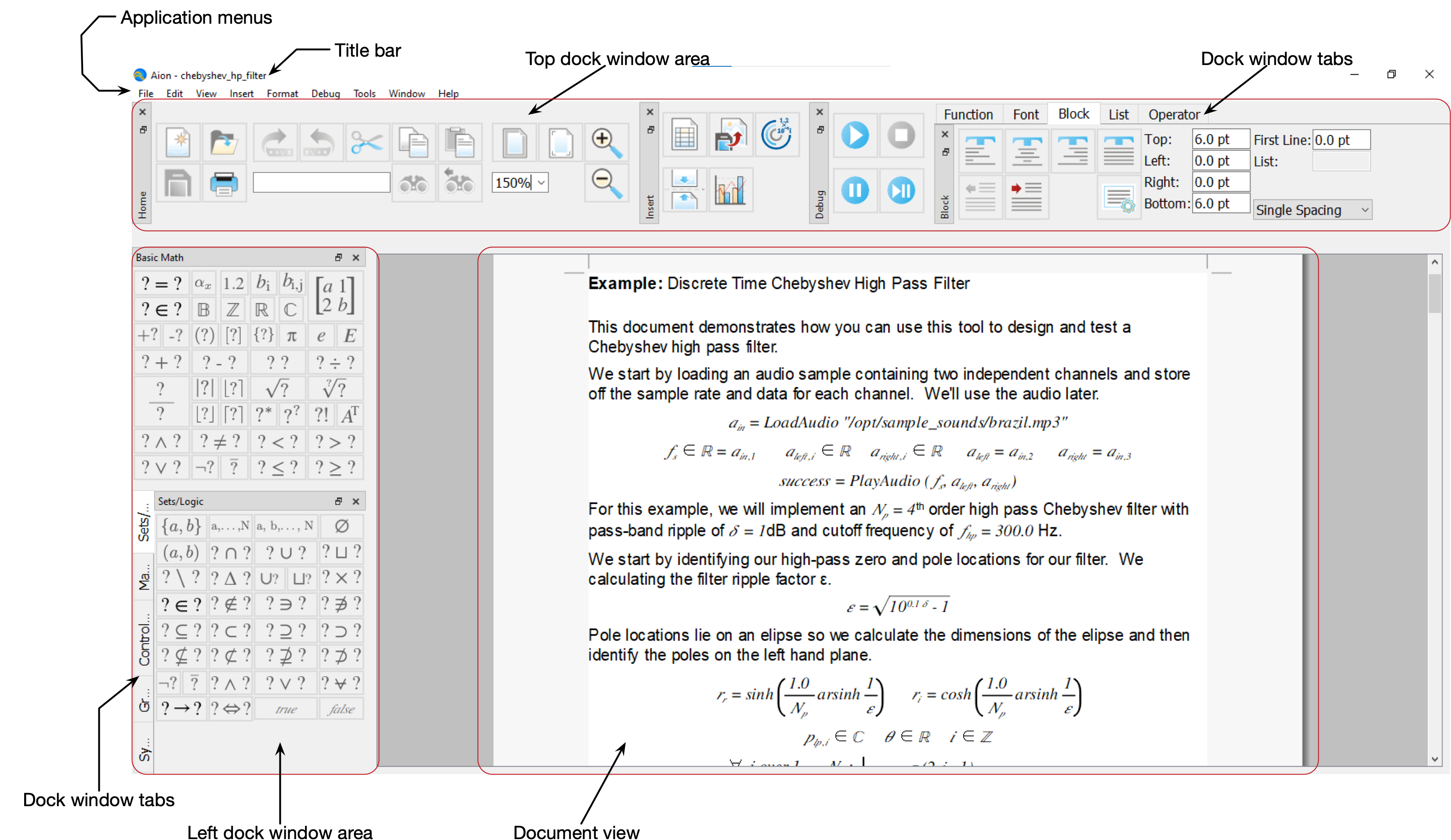
Figure 2 Aion on Windows 10¶

Figure 3 Aion on MacOS Catalina¶
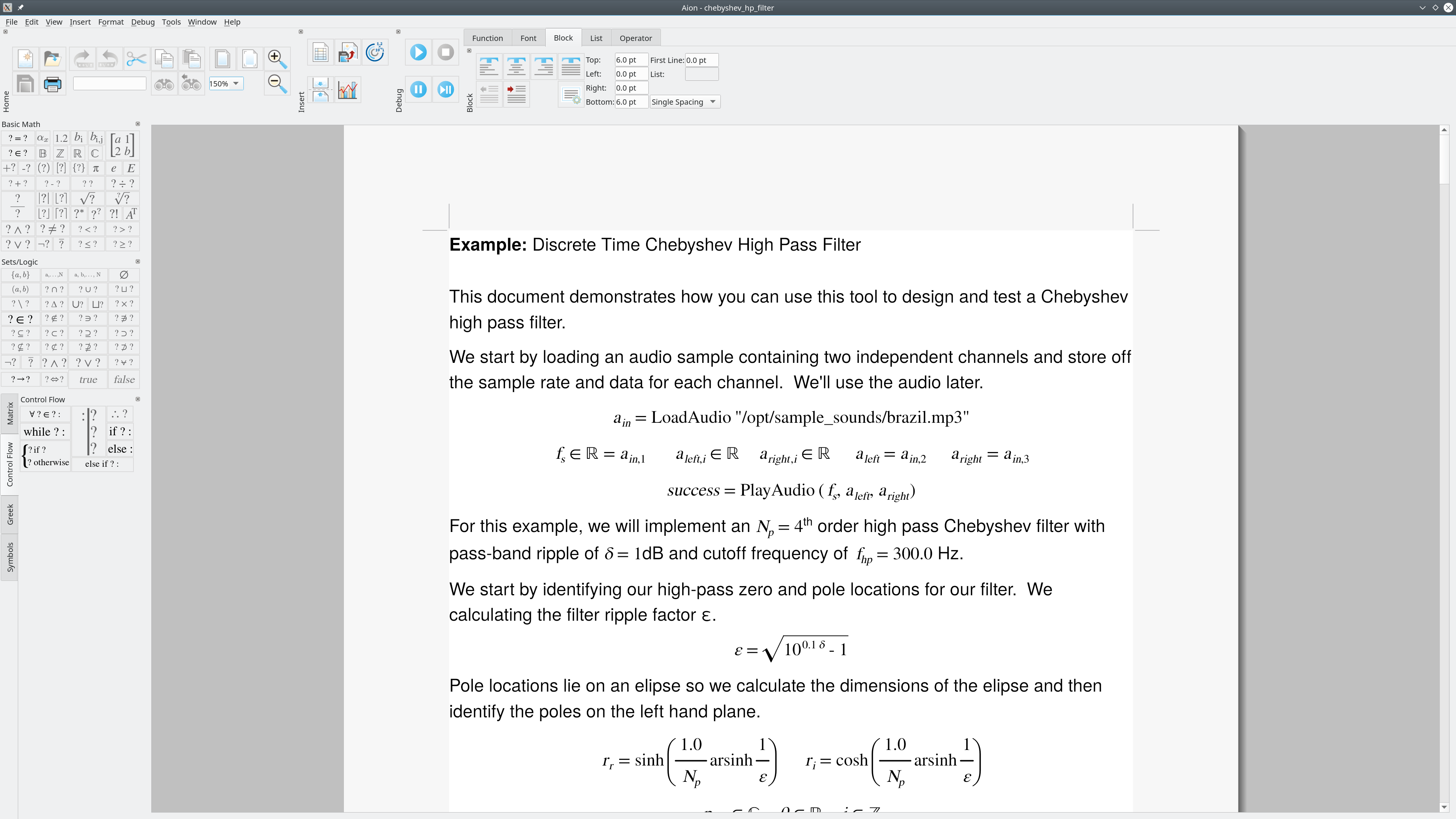
Figure 4 Aion on Linux (KDE)¶
The Aion user interface is similar on all three platforms.
The application main window can be broken down into a number of areas as shown in Figure 2:
The Aion title bar.
The Aion menus.
The dock areas.
Dock windows.
The editing area and document view.
The status bar (not shown above).
In addition, Aion will display a status bar only when compiling, exporting, or executing your algorithm or model and includes a number of dialogs and pop-up windows.
You can perform most operations either through the Aion menus, using the buttons and controls on the dock windows, through modal dialogs, and through a pop-up command window.
A small number of extremely common operations, such as cut and paste, undo/redo, etc. can also be performed using platform specific key sequences.
The sections that follow discuss different elements of the Aion user interface in detail.
The Title Bar¶
The title bar shows the product name and currently active file.
Editing Area, Document, And Document View¶
Most of the application main window contains the editing area. You use the editing area to create your algorithm or model, often referred to as a Document. The visible representation of your document that you can view and modify from the user interface is called The Document View. What you see in the document view will exactly match the output created when printing your model or algorithm to a file or when exporting your model or algorithm to a PDF file.
The user interface is similar to most common word processors such as Microsoft Word, Apple Pages, Open Office, or Libre Office.
Like most word processors, you can use the arrow keys, home, end, page up, and page down keys to navigate through the document view. Depending on the platform, the movement keys can be combined with the alt, or control/CTRL keys to move by Word, paragraph, etc. You can also use the mouse to position the cursor.
You can use the shift key in combination with the movement keys and mouse to select regions to be deleted, copied, or cut. Note that selections work somewhat differently on Aion compared to most Word Procesors. You will note that the selected range will adjust to impose several basic rules when selecting content within equations.
On Windows and Linux, you can also underline, boldface, or italize text using
CTRL-u, CTRL-b or CTRL-i respectively. On MacOS, you can use  -u,
-u,
 -b, or
-b, or  -i to underline, boldface, or italize text.
-i to underline, boldface, or italize text.
In addition, you can enter backslash commands directly by pressing the backslash (‘’\’’) key. See Command Window for details on entering and using backslash commands.
Through the menus, or backslash commands, you can add or remove tabs at the bottom of the document view and can use the tabs to maintain multiple views into the same document or separate views into multiple documents. You can also open new Aion windows that can either show different views into the same document or views into different documents. Each Aion window can have multiple tabs. Using multiple document views allows you to simultaneously view different sections of the same file or different files.
Right-clicking on a document view tab will also bring up a pop-up menu, shown in Figure 5, with a small number of useful controls.
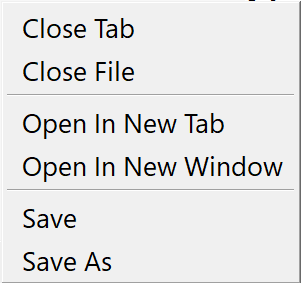
Figure 5 The Document Tab Popup Menu¶
Note that placing the cursor over mathematical elements may display a small window providing additional information such as the current value or type of a variable or an error associated with a mathematical element.
Dock Windows And Dock Areas¶
Almost all functions can be accessed from dock windows that can be placed along any of the four edges of the application window. The four edges where the dock windows can reside are called dock areas. On MacOS and Windows, the dock windows can also float.
You can also hide dock windows that you do not find useful by clicking on the
close button on the dock window. Alternately, you can hide or show a dock
window through the View | Dock | ... menu items. You can also show or hide
any dock through the command window.
Dock windows support both a horizontal and a vertical mode. When docked in the top or bottom dock area, or when floating, the dock windows will be displayed in their horizontal mode. When docked in the left or right dock areas, the dock windows will be displayed in their vertical mode. The available controls are the same in each display mode.
Lastly, you can stack dock windows on top of each other in any of the dock areas. When you do this, dock window tabs will appear. You can select which dock to show by clicking on the tab associated with the dock.
Note
There are a number of specialized dock windows that are available but hidden
by default. Used either the View | Dock | ... menu items or the command
window to enable these docks.
Command Window¶
You can use the command window, shown in Figure 7, to access almost all the functionality of Aion. All commands begin with a leading backslash, (‘’\’’). The command window will only provide commands that are allowed based on the the position of the cursor and application state.

Figure 7 The Command Window¶
For example, you can insert a fraction using the command \frac followed by
pressing space or return. To enter a backslash, enter a backslash twice
followed by a space or return.
In many cases, commands will be the same as those used in LaTeX. There may also be several commands that provide the same function, one matching what would be used in LaTeX and another more concise version.
Section Backslash Commands provides a complete list of commands.
Docks¶
Aion Docks are small groups of controls that provide functionality similar to tool bars or ribbon interfaces in other software packages. You can use docks to quickly access functions from the main window. Unlike tool bars or ribbon interfaces, you can relocate docks, hide or show docks, and stack docks on top of each other in order to adjust Aion to match the way you like to work. You can pick and choose the docks and place the docks in any of the four dock areas based on the position that works best for you. In addition, you can make docks float on Windows and Linux by double clicking on the dock’s title bar.
You can drag a dock to a new location by grabbing the dock’s title bar and moving the title bar to the new location. The selected dock will be repositioned at the new location. If you drag one dock on top of another dock, you can stack docks together. Once stacked, select the desired dock by clicking on the tab with the dock’s name. You can remove a dock from a stack simply by grabbing the dock by its title bar and dragging it to the new location.
When docks are dragged to a new position, such as from the top dock area to the left dock area, they will re-orient in order to better operate in their new position. The available controls remain the same but their positions in the dock will shift in order to make use the increased horizontal or vertical space. As an example Figure 49 and Figure 50 show the Home Dock in the horizontal and vertical orientations.
Aion supports a large number of different docks with only a handful made visible by default. You can enable or hide docks by selecting the dock in the View | Docks | … menu. You can also enable or hide any dock using the appropriate backslash command.
Home Dock¶
The Home Dock, shown in Figure 49, provides a number of common file and editing functions. The vertical orientation of the Home Dock is shown in Figure 50.
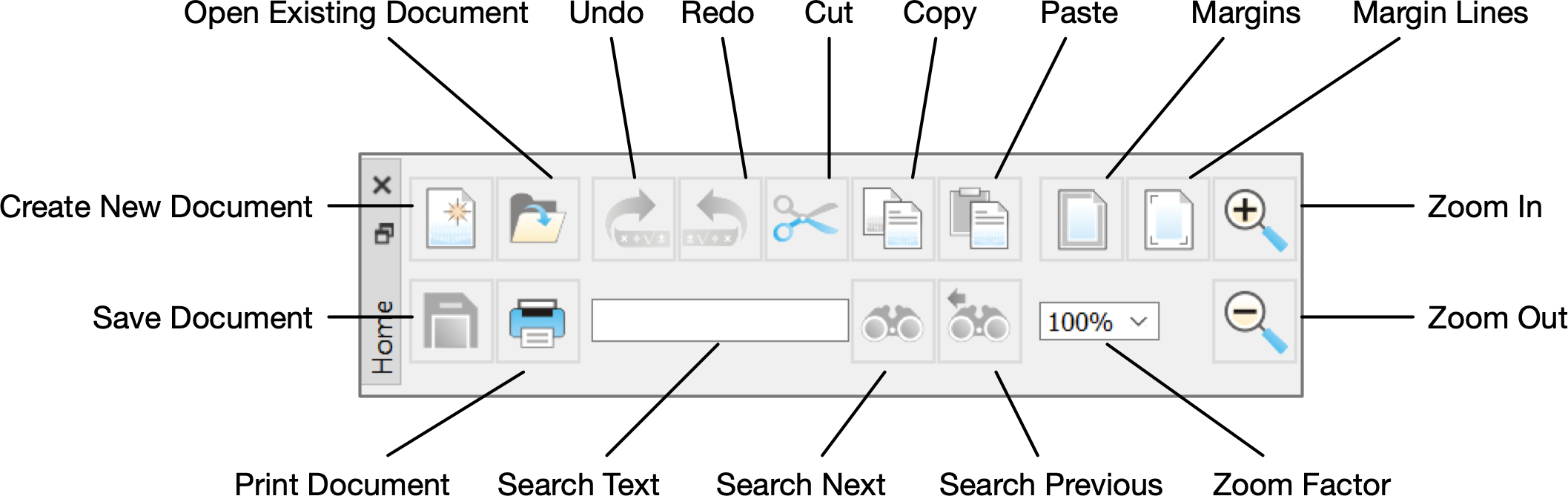
Figure 49 The Home Dock, Horizontal Orientation¶
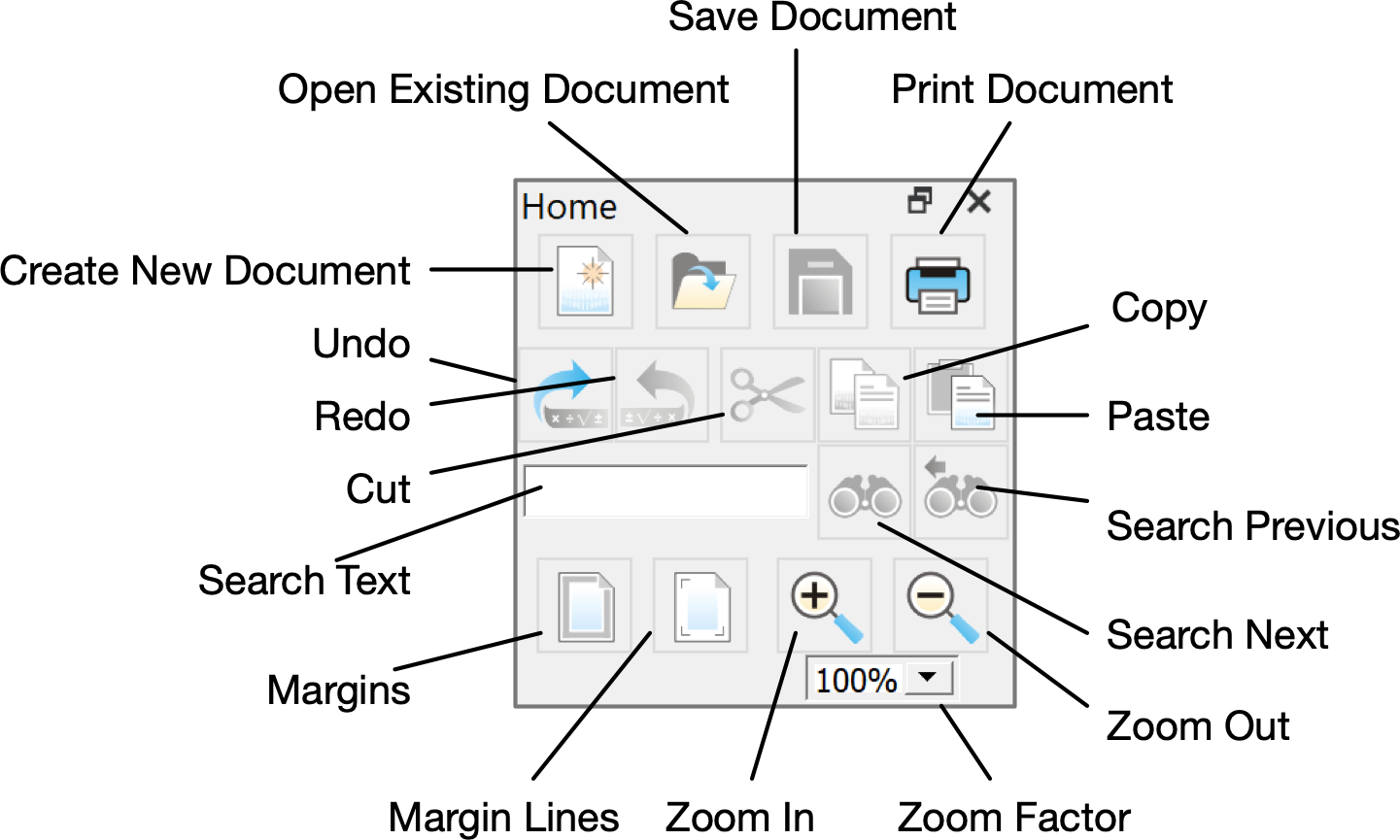
Figure 50 The Home Dock, Vertical Orientation¶
Insert Dock¶
You can use the Insert Dock, shown in Figure 51, to insert commonly used annotations and elements.
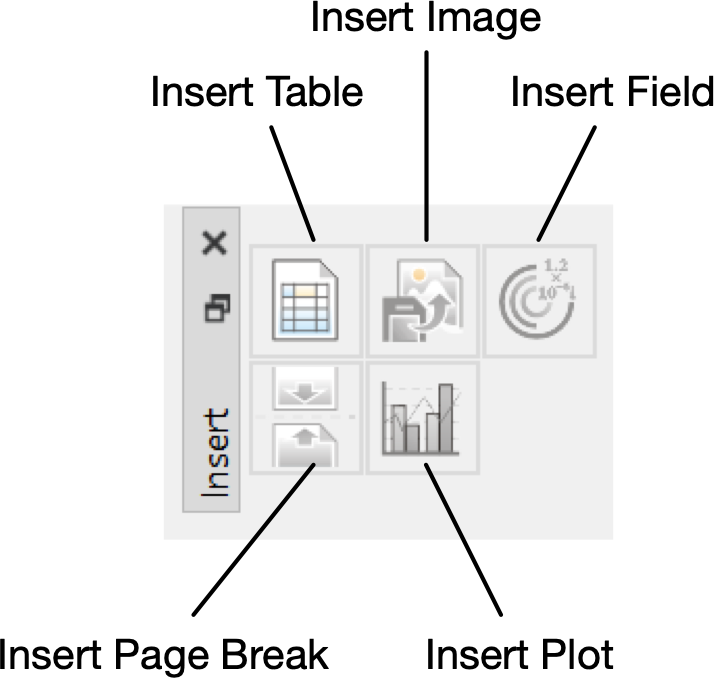
Figure 51 The Insert Dock, Horizontal Orientation¶
Debug Dock¶
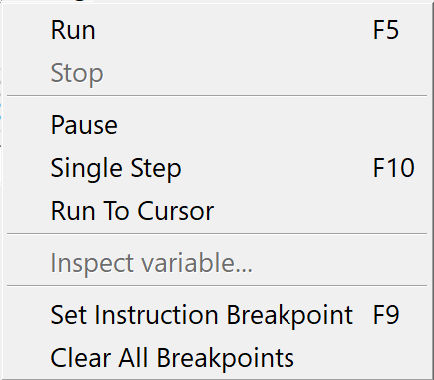
You can use the Debug Dock, shown in Figure 52, to perform common debugging functions.
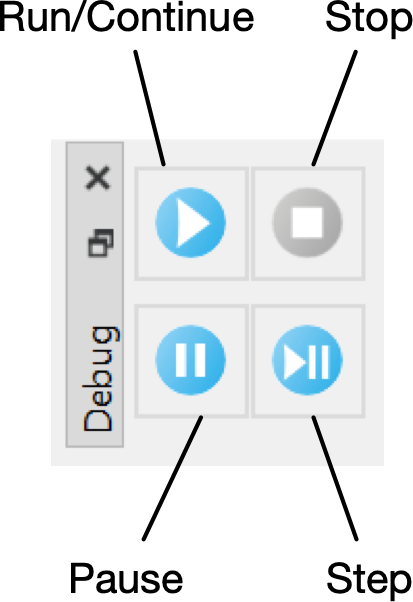
Figure 52 The Debug Dock, Horizontal Orientation¶
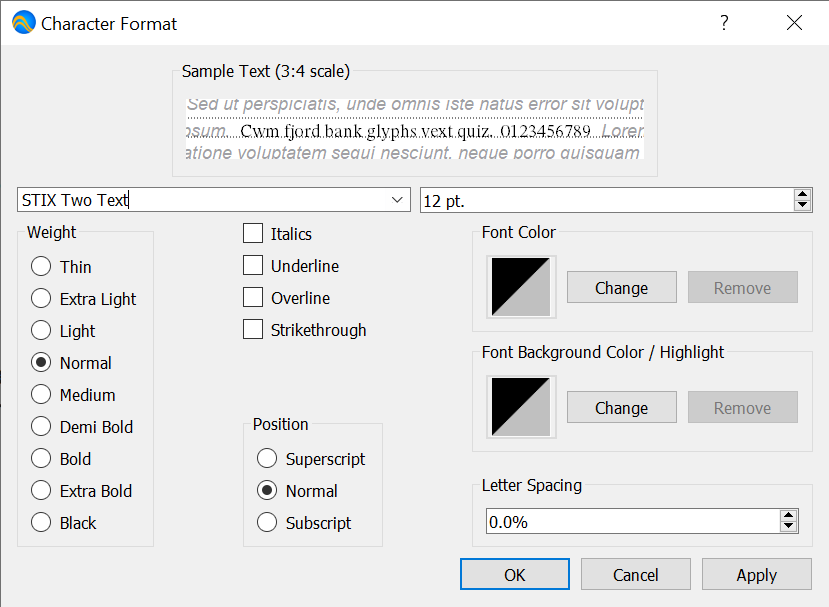
Font Dock¶
You can use the Font Dock, shown in Figure 53, to change either the font of currently selected text or the font of newly entered text. You can also use this dock to change the font used for mathematical elements.
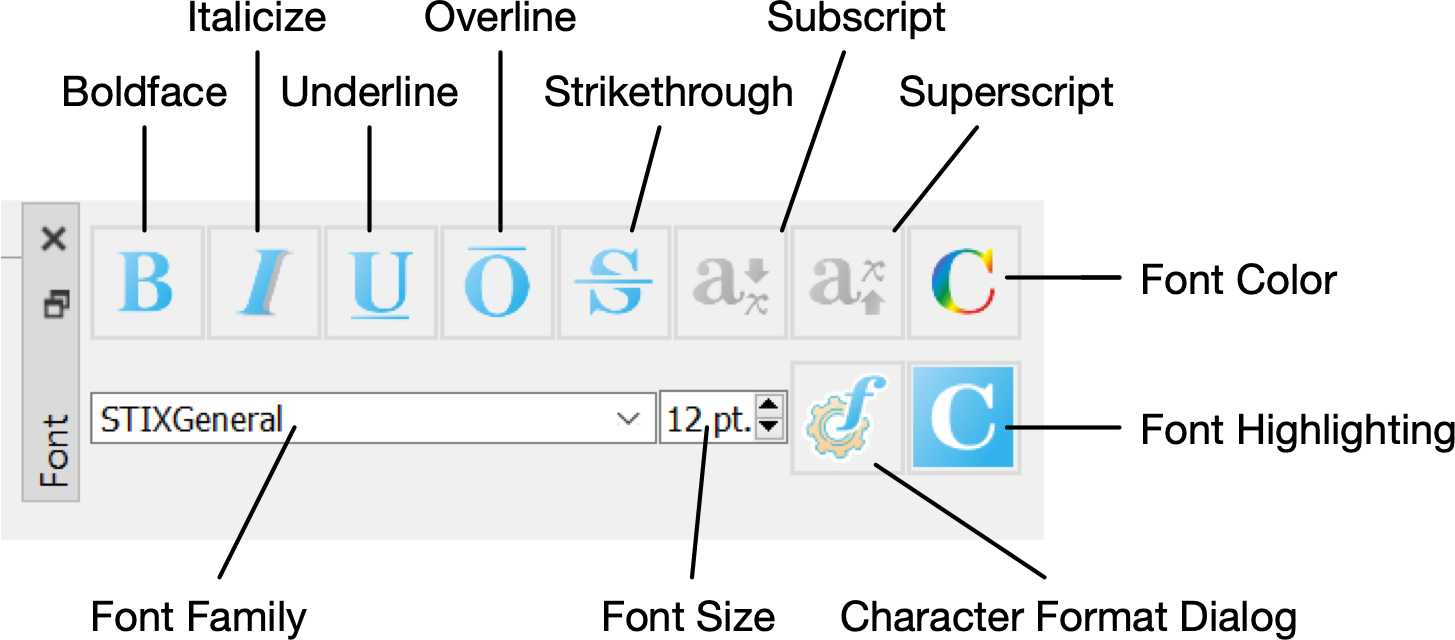
Figure 53 The Font Dock, Horizontal Orientation¶
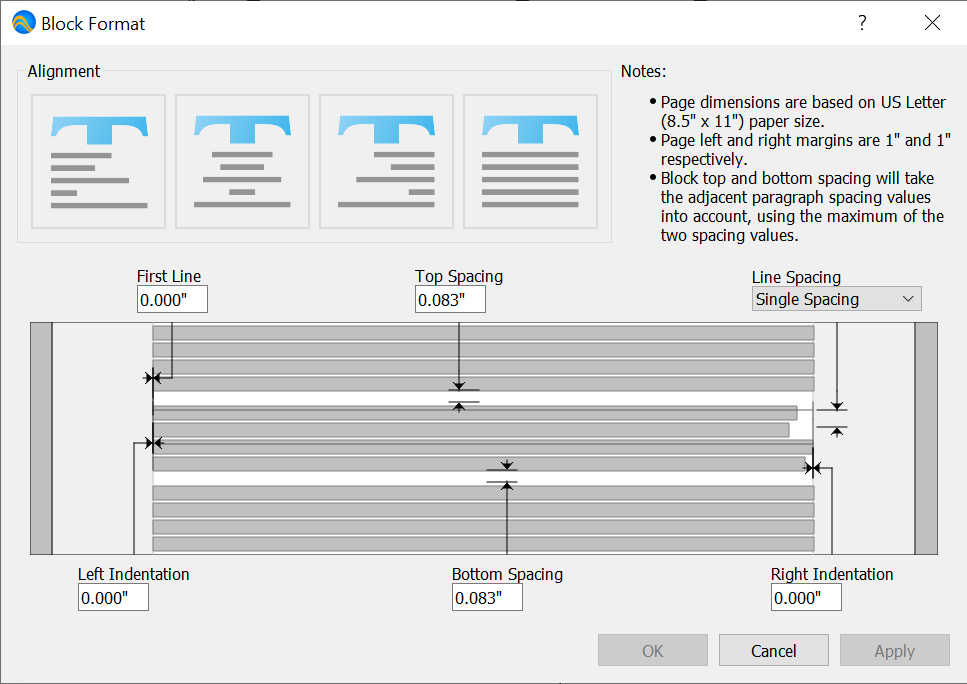
Block Dock¶
You can use the Block Dock, shown in Figure 54, to change paragraph and table indentation, spacing, and alignment.
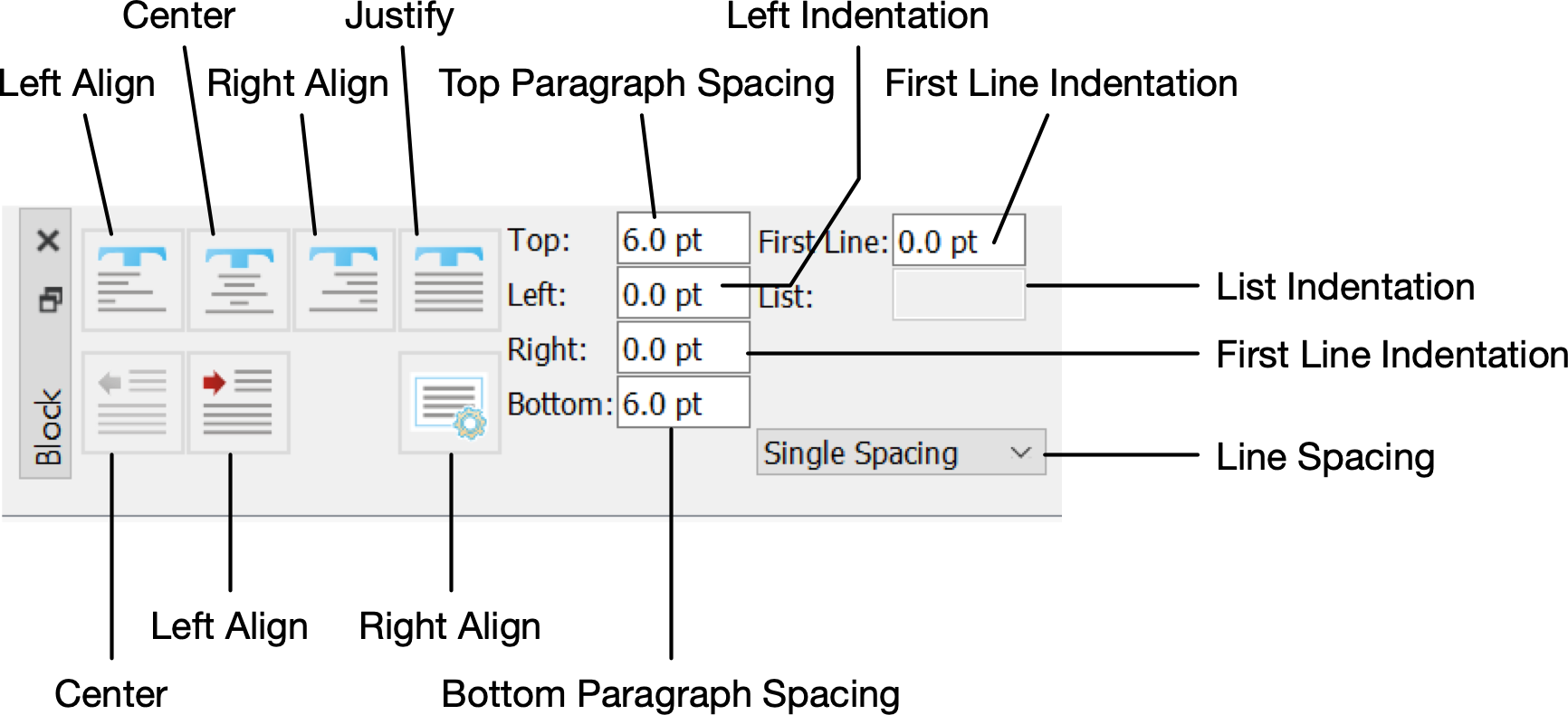
Figure 54 The Block Dock, Horizontal Orientation¶
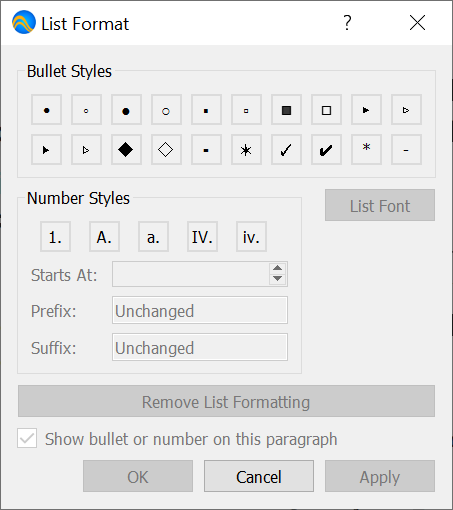
List Dock¶
You can use the List Dock, shown in Figure 55, to create or modify ordered and unordered lists.
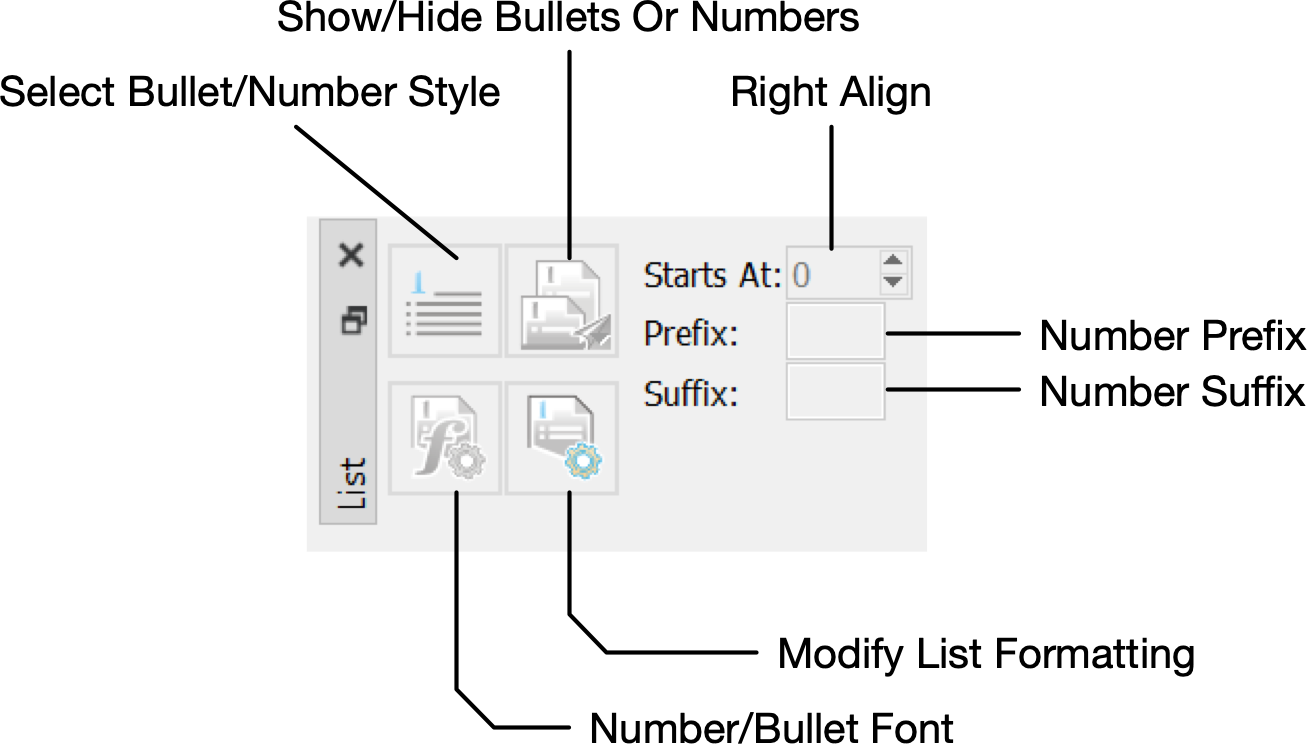
Figure 55 The List Dock, Horizontal Orientation¶
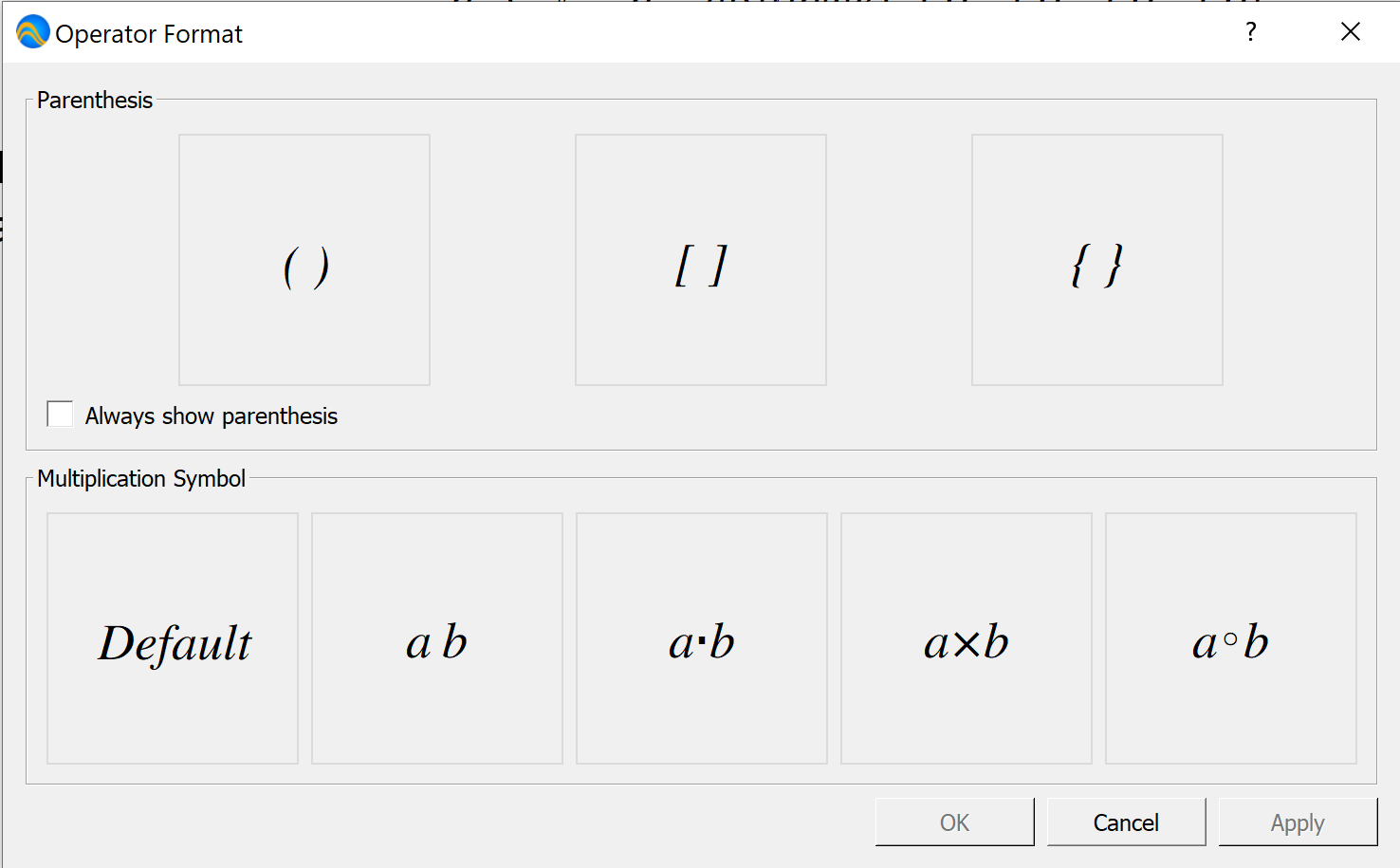
Operator Dock¶
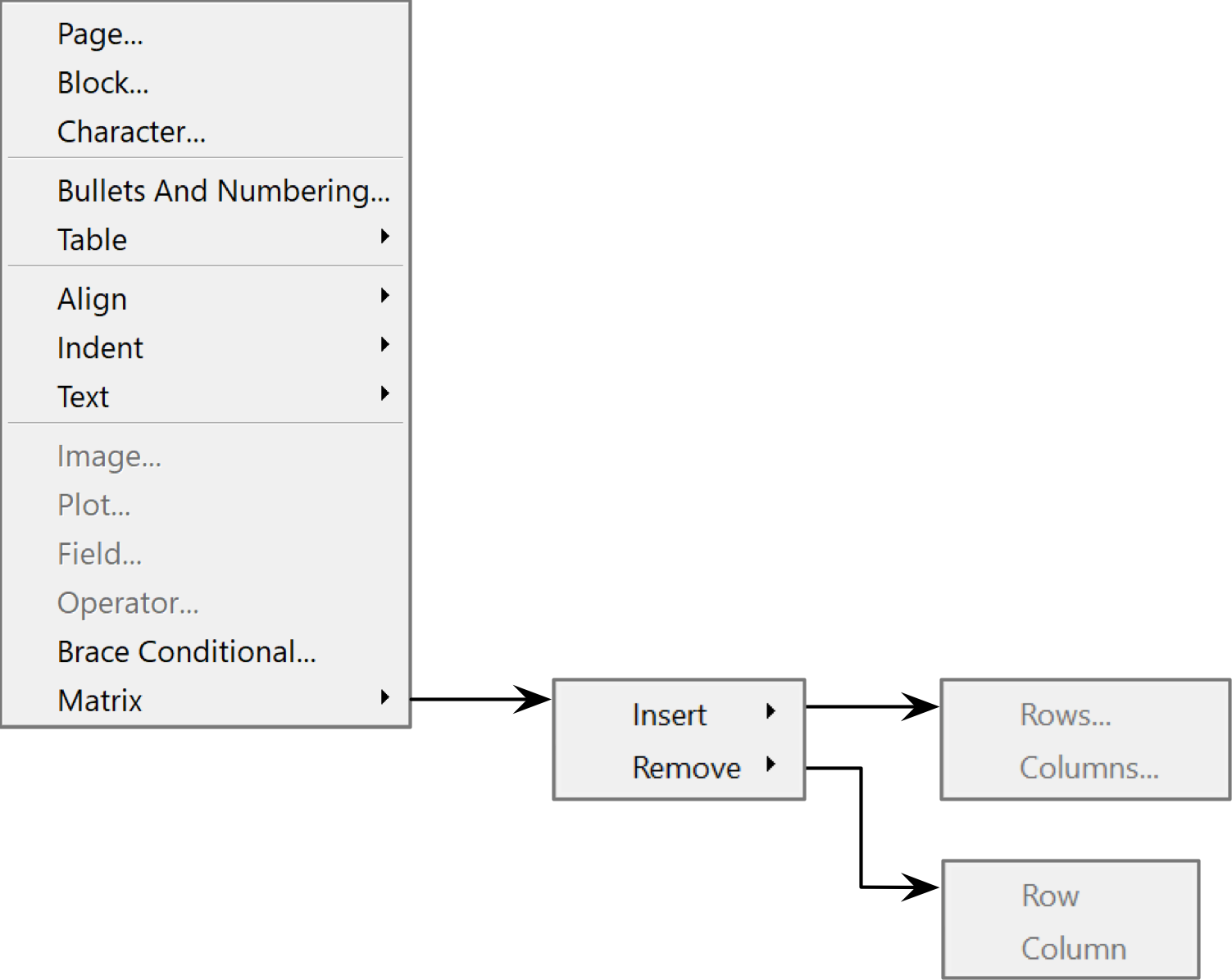
You can use the Operator Dock, shown in Figure 56, to create or modify the appearance of operators. Imposing parenthesis, brackets, or braces on an operator will also modify the order of operations for the operator.
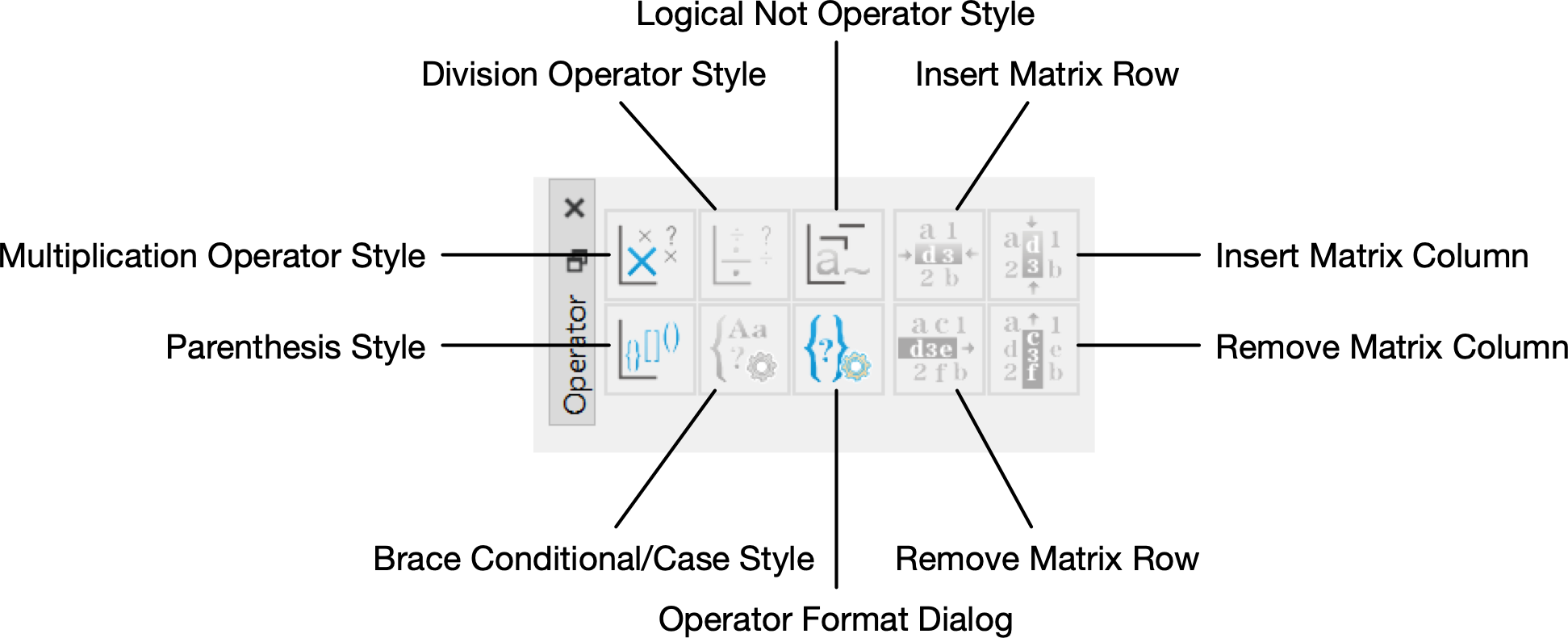
Figure 56 The Operator Dock, Horizontal Orientation¶
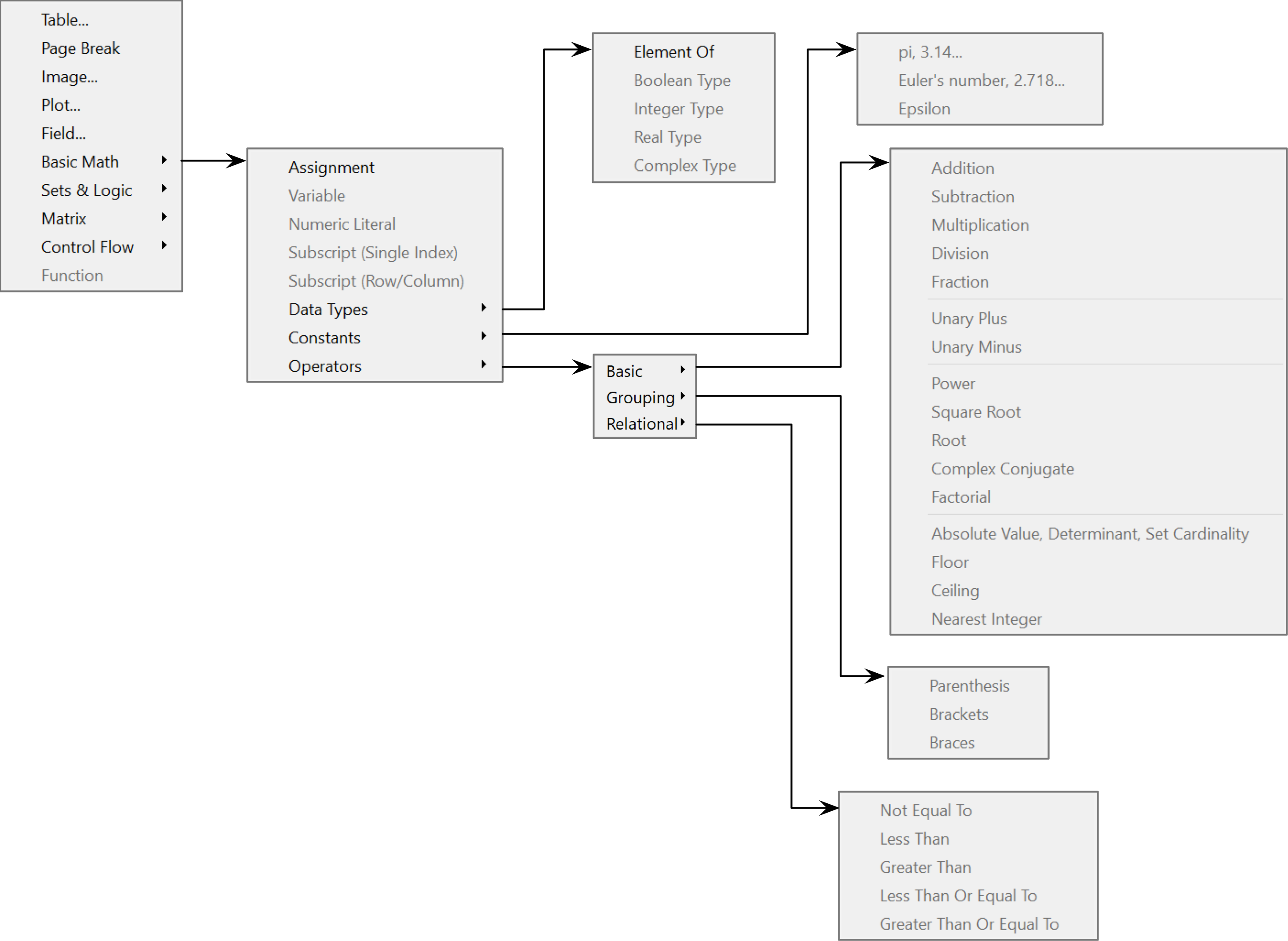
Basic Math Dock¶
You can use the Basic Math Dock, shown in Figure 57 and Figure 58, to insert commonly used mathematical operators. Several widely used operators are placed both on this dock and on docks dedicated to more specialized operations.
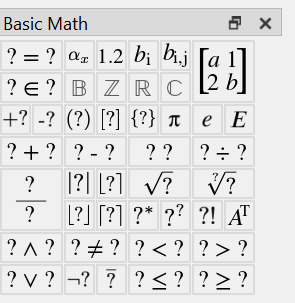
Figure 57 The Basic Math Dock, Vertical Orientation¶

Figure 58 The Basic Math Dock, Horizontal Orientation¶
Table 1 lists the various controls and their purpose.
Symbol |
Function |
|---|---|
\(? =\; ?\) |
Insert an assignment or test for equality. The meaning of this operator depends on context. |
\(a _ x\) |
Insert a variable name. |
\(1.2\) |
Insert a literal value, including complex values and strings. |
\(b _ i\) |
Insert a subscript with single dimension. You can use this operator with matricies and tuples. |
\(b _ { i,j }\) |
Insert a subscript with two dimensions. You can use this operator with matrices. |
\(\left [ \begin{matrix} a & 1 \\ 2 & b \end{matrix} \right ]\) |
Inserts a matrix or array. |
\(? \in\; ?\) |
Inserts an element of set operator. This operator can be used to force the type of a variable and can be used as a set relational operator. |
\(\mathbb{B}\) |
Inserts a boolean set type. |
\(\mathbb{Z}\) |
Inserts an integer set type. |
\(\mathbb{R}\) |
Inserts a real set type. |
\(\mathbb{C}\) |
Inserts a complex set type. |
\(\pi\) |
Inserts the special value \(\pi\). |
\(e\) |
Inserts Euler’s number, \(e\). |
\(\mathit{E}\) |
Inserts the machine epsilon for real values. |
\(? + ?\) |
Inserts an addition operator. |
\(? - ?\) |
Inserts a subtraction operator. |
\(? \; ?\) |
Inserts a multiplication operator. |
\(? \div ?\) |
Inserts a division (obelus) operator. |
\(\frac{?}{?}\) |
Inserts a division (fraction) operator. |
\(\left | ? \right |\) |
Insert an absolute value, magnitude, set cardinality, or matrix determinant operator. Exact behavior depends on context. |
\(\left \lfloor ? \right \rceil\) |
Inserts a nearest integer value operator. Calculates the nearest integer to a given value. |
\(\left \lfloor ? \right \rfloor\) |
Inserts a floor operator. Calculates the closest integer equal to or less than the the supplied value. |
\(\left \lceil ? \right \rceil\) |
Inserts a ceiling operator. Calculates the closest integer greater than or equal to the supplied value. |
\(\sqrt{?}\) |
Inserts a square root operator. Calculates the square root of a value. |
\(\sqrt[?]{?}\) |
Inserts an n th root operator. Calculates the n th root of a value. |
\(? ^ {*}\) |
Inserts a complex conjugate operator. Calculates the complex conjugate of a value. If applied to a matrix, this operator will calculate the per-element complex conjugate of each element without performing a transpose. |
\(? ^ {T}\) |
Inserts a transpose operator. Performs a matrix transpose operation. |
\(? ^ {H}\) |
Inserts a conjugate transpose or Hermitian transpose operator. This operator is mathematically equivalent to \(\left ( ? ^ {T} \right ) ^ {*}\). |
\(? \neq \; ?\) |
Inserts a not-equal-to relational operator. |
\(? < \; ?\) |
Inserts a less-than relational operator. |
\(? > \; ?\) |
Inserts a greater-than relational operator. |
\(? > \; ?\) |
Inserts a greater-than relational operator. |
\(? \leq \; ?\) |
Inserts a less-than or equal to relational operator. |
\(? \geq \; ?\) |
Inserts a greater-than or equal to relational operator. |
\(? \; \land \; ?\) |
Inserts a logical ‘’and’’ operator. |
\(? \; \lor \; ?\) |
Inserts a logical ‘’or’’ operator. |
\(\neg ?\) |
Inserts a unary logical ‘’not’’ operator. |
\(\overline{?}\) |
Inserts an overbar not operator. |
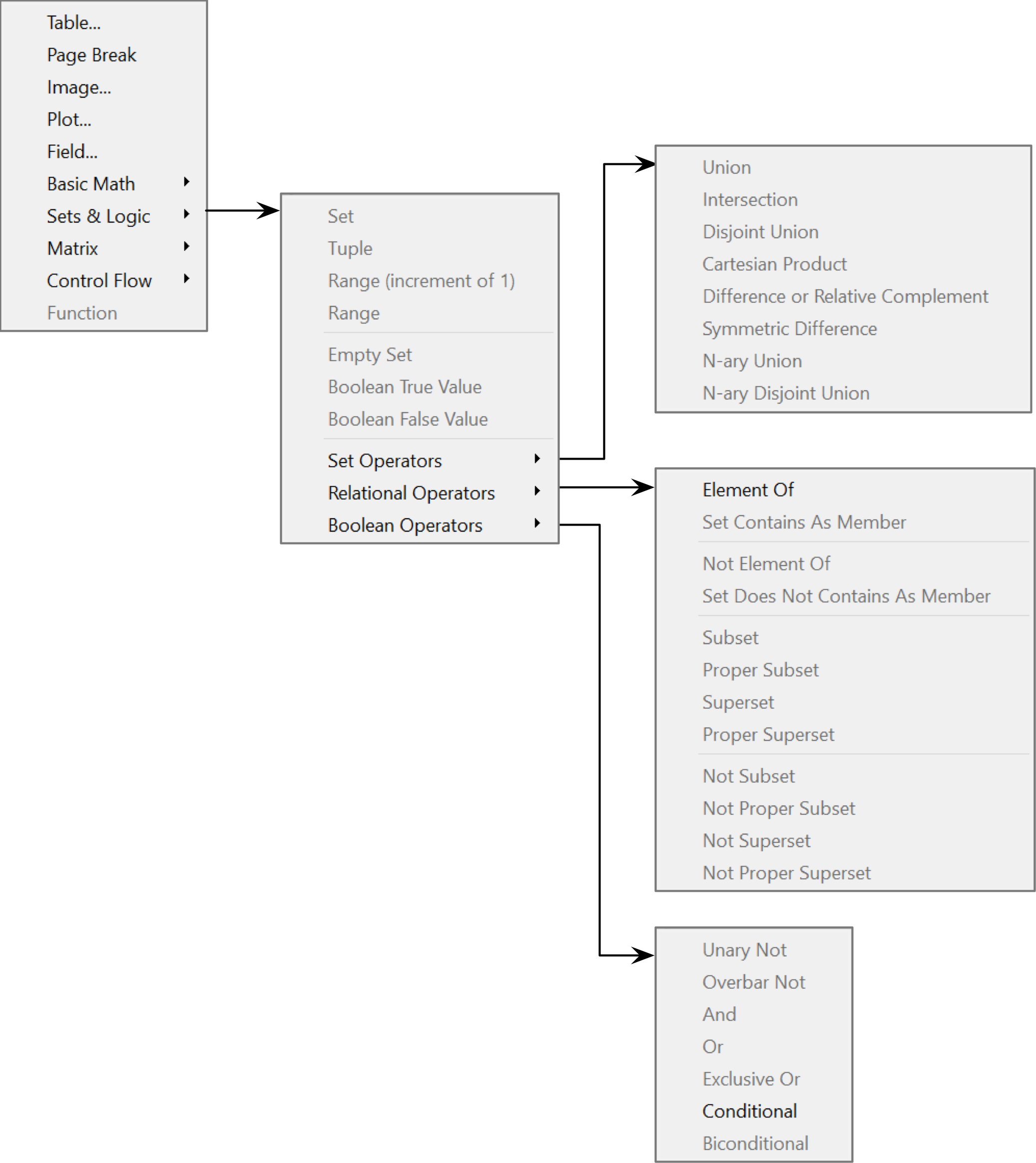
Sets/Logic Dock¶
You can use the Sets/Logic Dock, shown in Figure 59 and Figure 60, to insert mathematical operators and values associated with sets and boolean algebra.
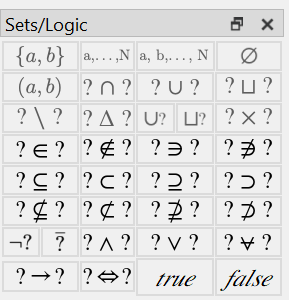
Figure 59 The Sets/Logic Dock, Vertical Orientation¶

Figure 60 The Sets/Logic Dock, Horizontal Orientation¶
Table 2 lists the various controls and their purpose.
Symbol |
Function |
|---|---|
\(\left \lbrace a, b \right \rbrace\) |
Inserts a literal set containing other values. |
\(a, \ldots, N\) |
Inserts a range that implicitly increments by 1. |
\(a, b, \ldots, N\) |
Inserts a range that explicitly increments by \(b - a\). |
\(\varnothing\) |
Inserts an empty set special value. |
\(\left ( a. b \right )\) |
Inserts a literal tuple, triple, etc. containing other values. |
\(? \; \cap \; ?\) |
Inserts a binary set intersection operator. |
\(? \; \cup \; ?\) |
Inserts a binary set union operator. |
\(? \; \sqcup \; ?\) |
Inserts a binary set disjoint union operator. |
\(? \; \setminus \; ?\) |
Inserts a binary set relative difference operator. |
\(? \; \Delta \; ?\) |
Inserts a binary set symmetric difference operator. |
\(\bigcup \; ?\) |
Inserts an nary set union difference operator. |
\(\bigsqcup \; ?\) |
Inserts an nary set disjoint union difference operator. |
\(? \; \times \; ?\) |
Inserts a binary cartesian product operator. |
\(? \in\; ?\) |
Inserts an element of set operator. This operator can be used to force the type of a variable and can be used as a set relational operator. |
\(? \notin\; ?\) |
Inserts a not element of set relational operator. You can use this operator to check if a value is not contained within a set. |
\(? \ni\; ?\) |
Inserts a set contains relational operator. You can use this operator to check if a set contains a value. |
\(? \not\ni\; ?\) |
Inserts a set does not contain relational operator. You can use this operator to check if a set does not contain a value. |
\(? \subseteq\; ?\) |
Inserts a subset relational operator. |
\(? \subset\; ?\) |
Inserts a proper subset relational operator. |
\(? \supseteq\; ?\) |
Inserts a superset relational operator. |
\(? \supset\; ?\) |
Inserts a proper superset relational operator. |
\(? \nsubseteq\; ?\) |
Inserts a not subset relational operator. |
\(? \not\subset\; ?\) |
Inserts a not proper subset relational operator. |
\(? \nsupseteq\; ?\) |
Inserts a not superset relational operator. |
\(? \not\supset\; ?\) |
Inserts a not proper superset relational operator. |
\(\neg ?\) |
Inserts a unary not operator. |
\(\overline{?}\) |
Inserts an overline not operator. |
\(? \;\land\; ?\) |
Inserts a logical and operator. |
\(? \;\lor\; ?\) |
Inserts a logical or operator. |
\(? \, \lor\mspace{-17mu}-\; ?\) |
Inserts a logical exclusive or operator. |
\(? \rightarrow\; ?\) |
Inserts a logical conditional operator. You can also used this operator to conditionally evaluate the right hand expression. |
\(? \Leftrightarrow\; ?\) |
Inserts a logical biconditional operator. |
\(true\) |
Inserts a logical ‘’true’’ special value. You can also use any non-zero numeric value for ‘’true’’. |
\(false\) |
Inserts a logical ‘’false’’ special value. You can also use a numeric value of 0 for ‘’false’’. |
Matrix Dock¶
You can use the Matrix Dock, shown in Figure 61 and Figure 62, to insert matrix specific operators.
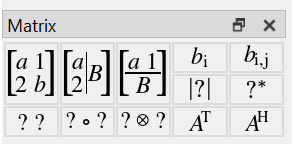
Figure 61 The Matrix Dock, Vertical Orientation¶
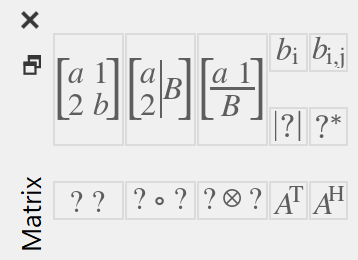
Figure 62 The Matrix Dock, Horizontal Orientation¶
Table 3 lists the various controls and their purpose.
Symbol |
Function |
|---|---|
\(\left [ \begin{matrix} a & 1 \\ 2 & b \end{matrix} \right ]\) |
Inserts a matrix or array. |
\(\left [ \begin{array}{c} a \\ 2 \end{array} \Big\vert\; B \right ]\) |
Inserts a matrix combine operator, combining matrices left-to-right. |
\(\left [ \frac{a \; 1}{B} \right ]\) |
Inserts a matrix combine operator, combining matrices top-to-bottom. |
\(b _ i\) |
Insert a subscript with single dimension. You can use this operator with matricies and tuples. The operator will reference elements in reading order, by columns, then by rows. |
\(b _ { i,j }\) |
Insert a subscript with two dimension. |
\(\left | ? \right |\) |
Insert a determinate operator. You can also use this operator to calculate absolute value, magnitude, or set cardinality. The exact behavior depends on context. |
\(? ^ {*}\) |
Inserts a complex conjugate operator. Calculates the complex conjugate of each element of a matrix without also performing a transpose. You can also use this operator to calculate the complex conjugate of other values. |
\(? \; ?\) |
Inserts a multiplication operator. |
\(? \; \circ \; ?\) |
Inserts a Hadamard product operator. |
\(? \; \otimes \; ?\) |
Inserts a Kronecker product operator. |
\(? ^ {T}\) |
Inserts a transpose operator. Performs a matrix transpose operation. |
\(? ^ {H}\) |
Inserts a conjugate transpose or Hermitian transpose operator. This operator is mathematically equivalent to \(\left ( ? ^ {T} \right ) ^ {*}\). |
Control Flow Dock¶
You can use the Control Flow Dock, shown in Figure 63, to insert specialized operators used to define complex algorithms that require iteration or conditional evaluation.
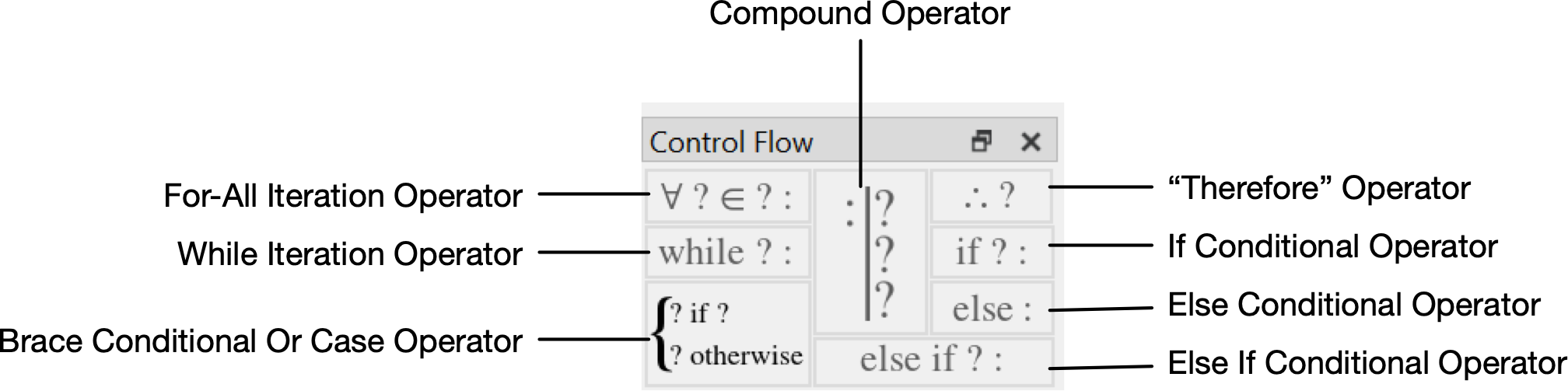
Figure 63 Control Flow Dock, Vertical Orientation¶
Function Dock¶
You can use the Function Dock, shown in Figure 64 and Figure 65, to simplify the insertion of Aion functions into your algorithm or model.
You can use the ‘’search’’ line to search for functions by keyword. Adding additional keywords will narrow the search.
You can use the 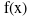 button to either define a user
defined function or use a function.
button to either define a user
defined function or use a function.
You can use the 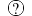 button to obtain help about the currently
selected function.
button to obtain help about the currently
selected function.
You can insert a selected standard function by double clicking on it or by
clicking on the insert standard function icon, 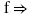 .
.

Figure 64 Function Dock, Horizontal Orientation¶
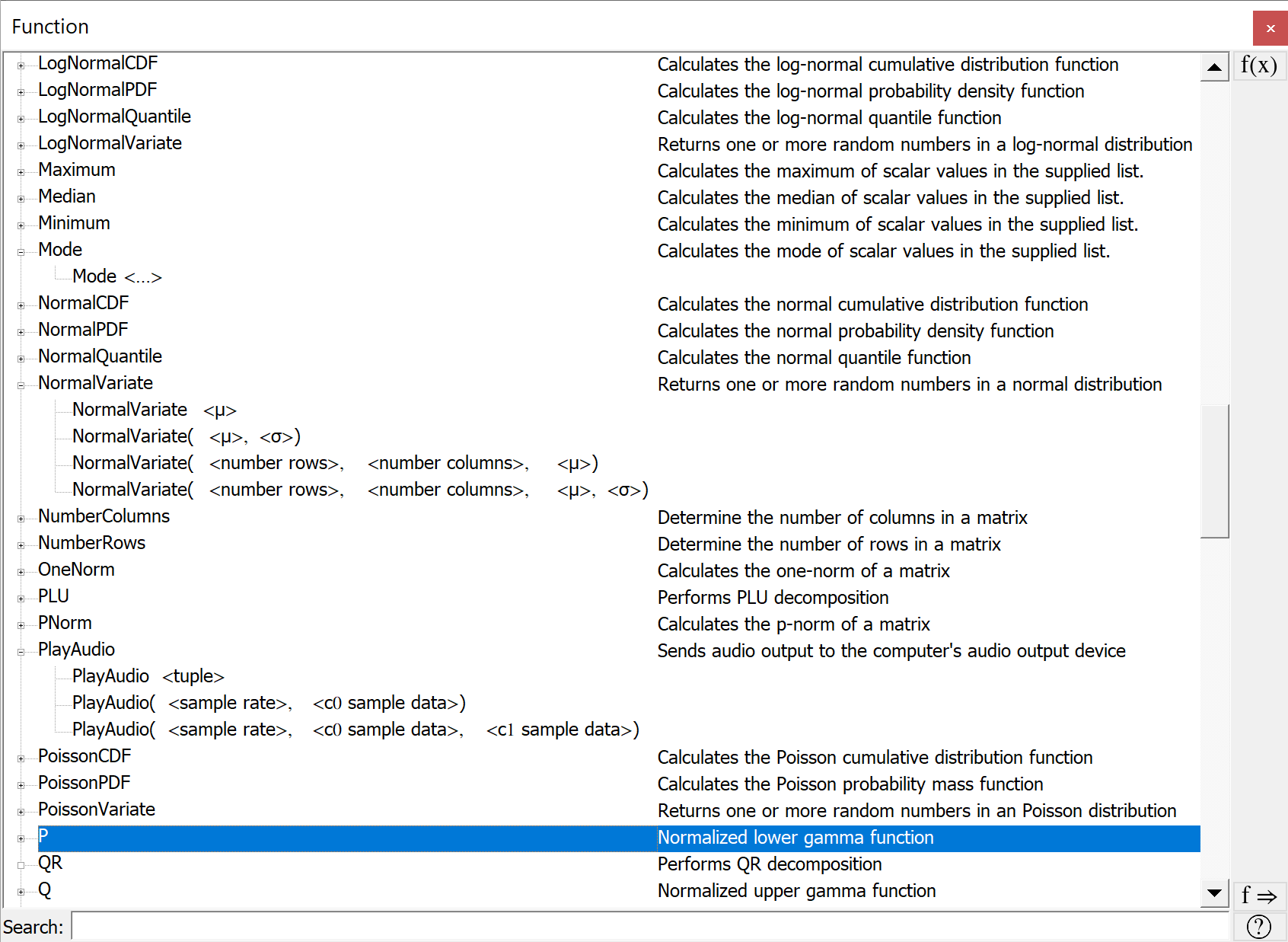
Figure 65 Function Dock, Floating¶
Greek Dock¶
You can use the Greek Dock, shown in Figure 66, to easily insert Greek characters into text or into mathematical elements.

Figure 66 Greek Dock, Vertical Orientation¶
Symbols Dock¶
You can use the Symbols Dock, shown in Figure 67, to easily insert special symbols into text or into mathematical elements. Note that some symbols can only be inserted into text and will be disabled when the cursor is in a mathematical element.
Figure 67 Symbols Dock, Vertical Orientation¶
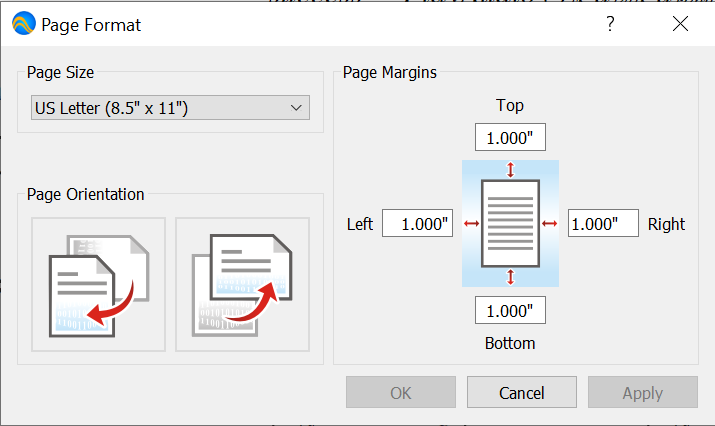
Page Dock¶
You can use the Page Dock, shown in Figure 68, to adjust the page size, page orientation, and page margins.
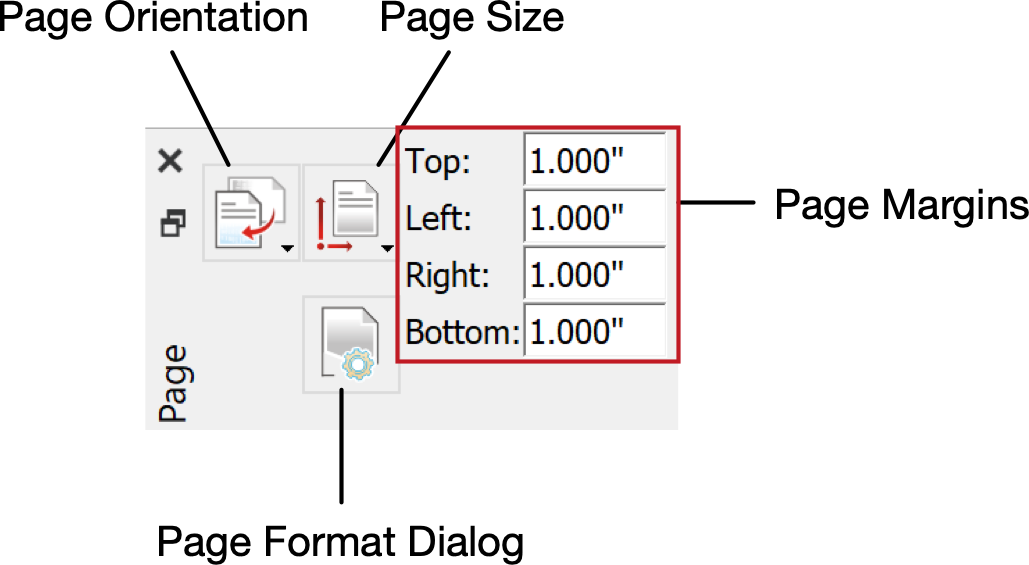
Figure 68 Page Dock, Horizontal Orientation¶
Table Dock¶
You can use the Table Dock, shown in Figure 69, to adjust table global parameters such as the alignment of the table on the page and default settings for table cells.
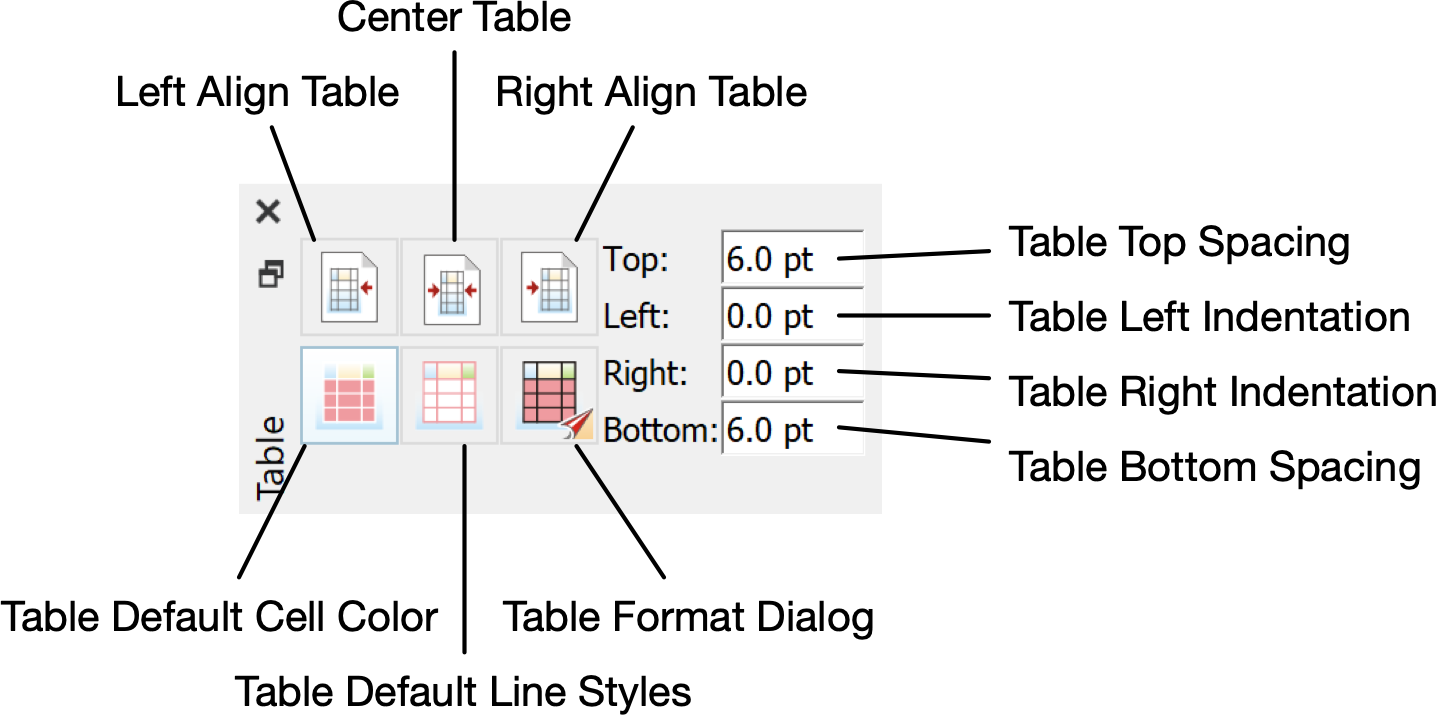
Figure 69 Table Dock, Horizontal Orientation¶
Table Cell Dock¶
You can use the Table Cell Dock, shown in Figure 70, to adjust the characteristics of individual table cells or groups of table cells. You can use this dock to quickly add and remove rows and columns, merge or unmerge cells, and change the appearance of cells within the document.
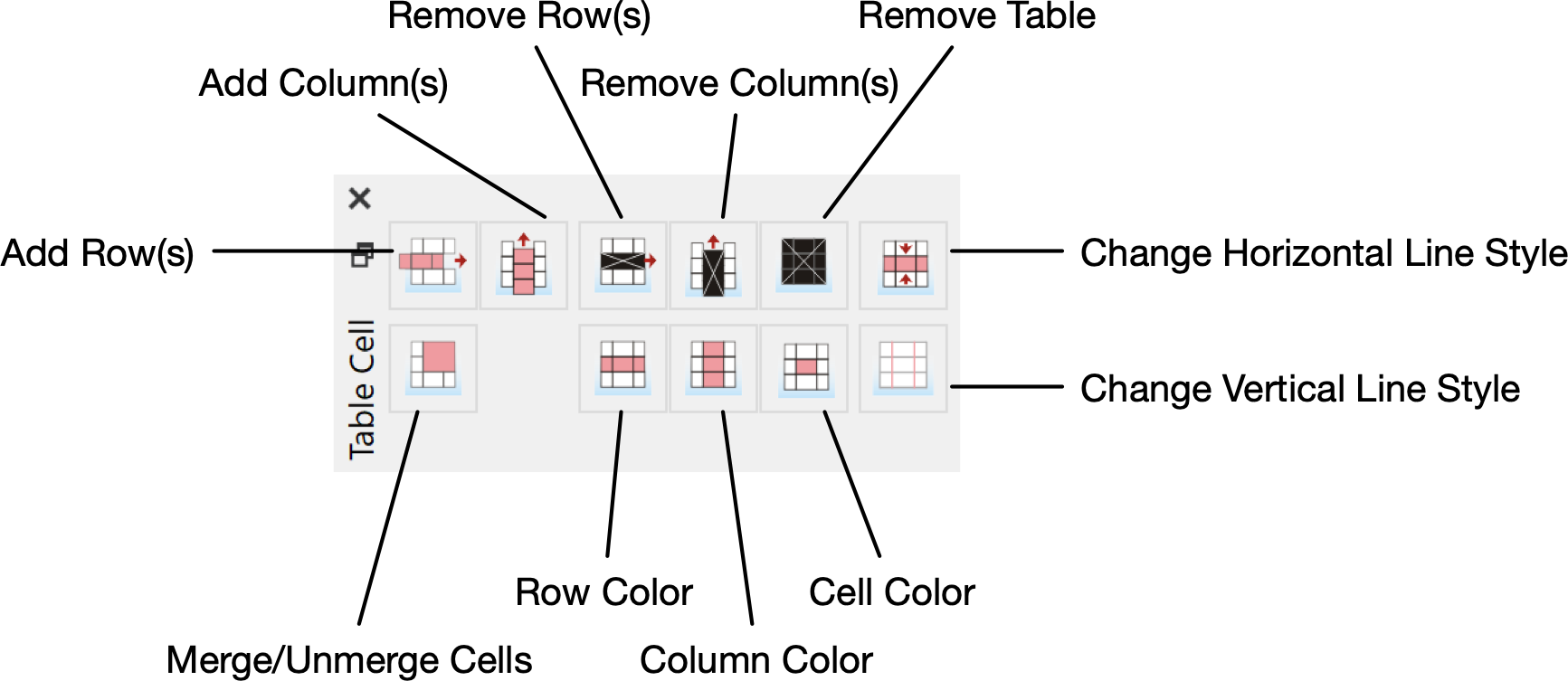
Figure 70 Table Cell Dock, Horizontal Orientation¶
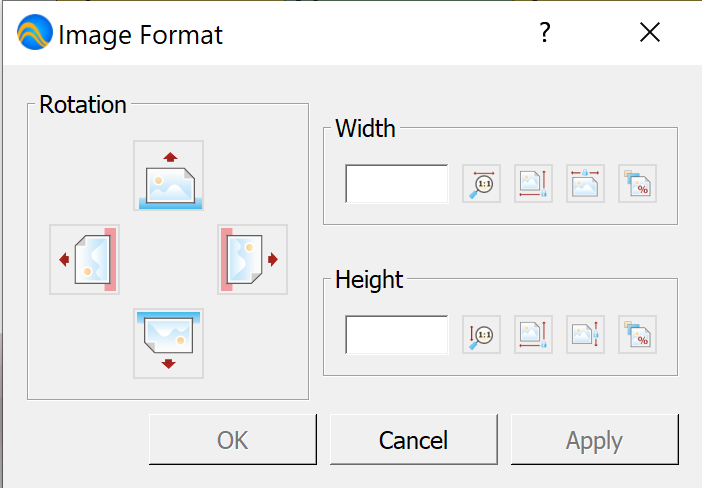
Image Dock¶
You can use the Image Dock, shown in Figure 71, to rotate and scale images.
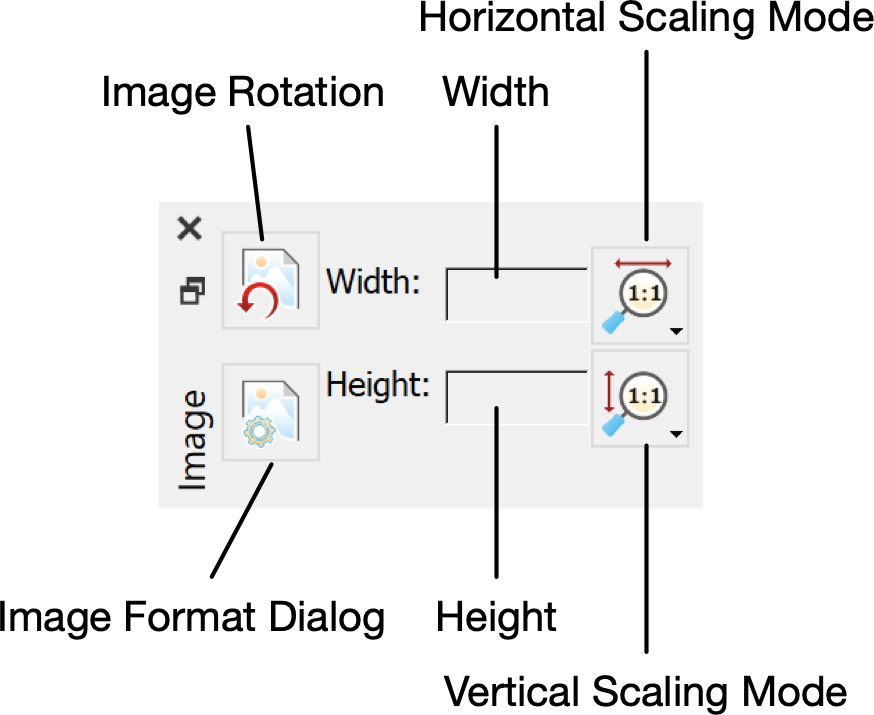
Figure 71 Image Dock, Horizontal Orientation¶
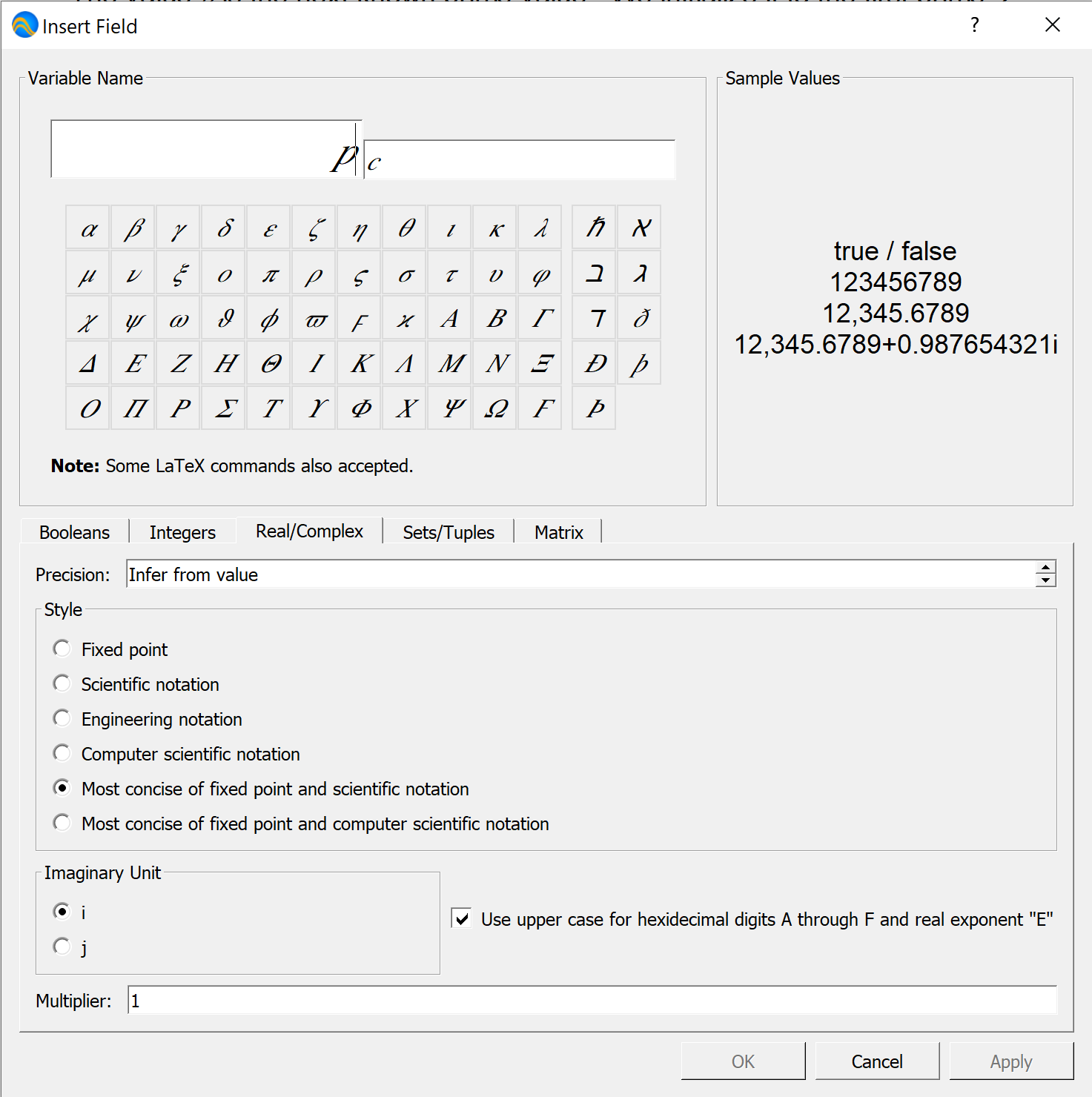
Field Dock¶
You can use the Field Dock, shown in Figure 72, to adjust the characteristics of fields used to display the results of your model or algorithm.

Figure 72 Field Dock, Horizontal Orientation¶
Status Bar¶
Aion will display a status bar along the bottom of the screen under three scenarios:
When compiling or exporting your document.
When running or debugging your algorithm or model.
After an error occurs.
When compiling or exporting your document, the status bar will show progress to completion.
When running or debugging your algorithm or model, the status bar will pulsate to indicate activity.
When an error occurs, the status bar will display a brief message explaining the error. Note that the mathematical element(s) where errors were found will be highlighted in red. Hovering over a highlighted element will provide additional details regarding the error.



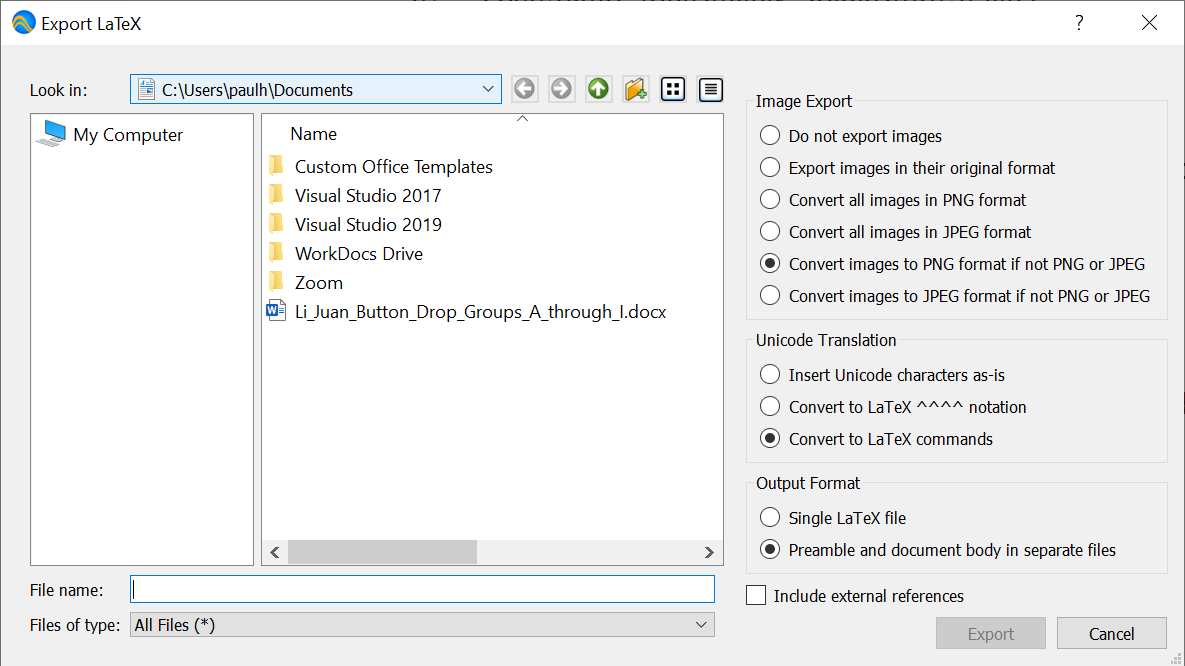

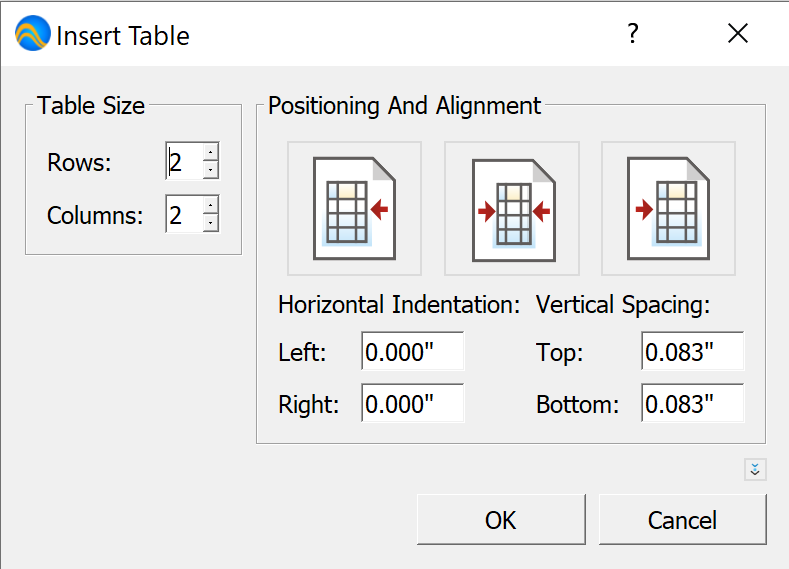
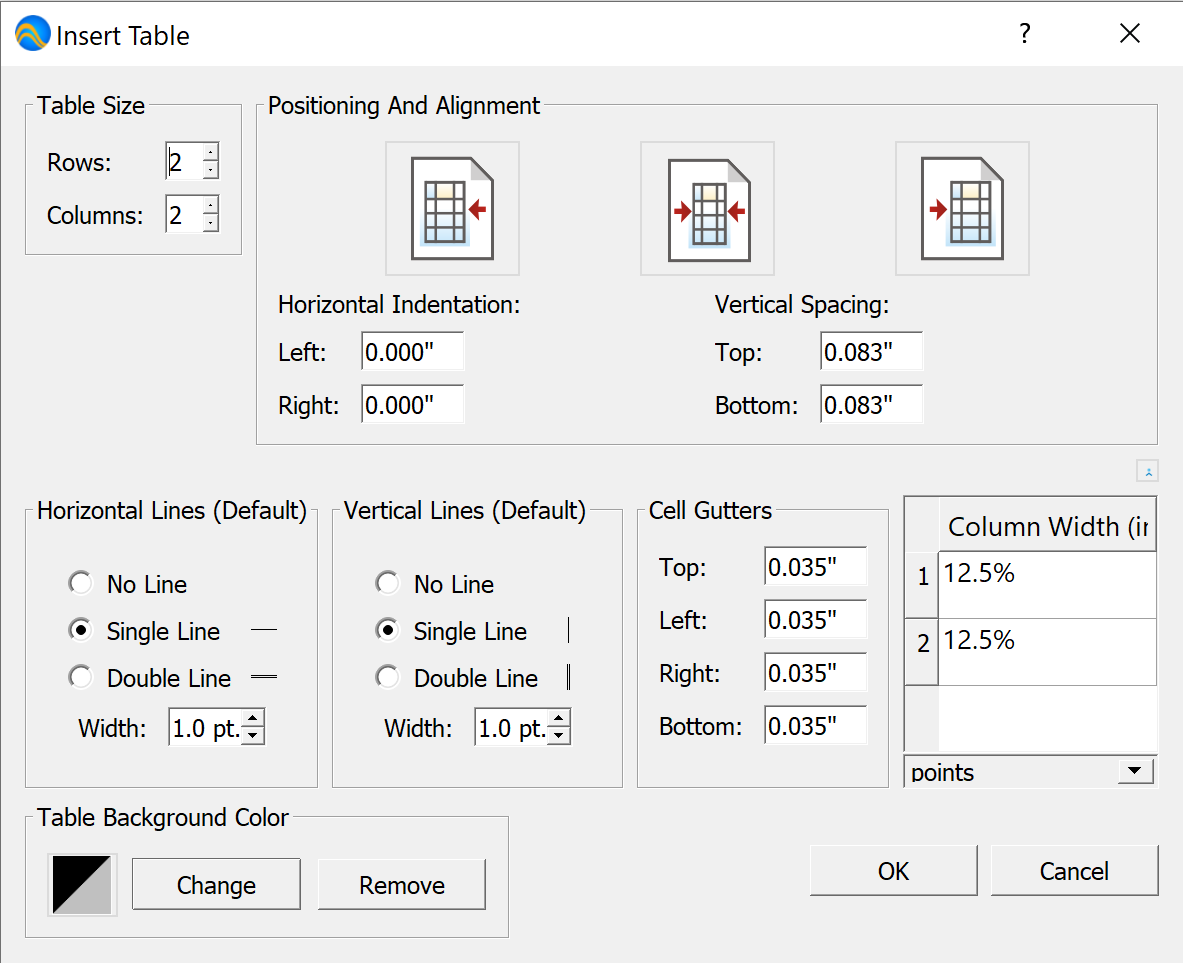
 ), will display the advanced
settings you can use to control column widths, line styles, and cell gutter
settings as shown in
), will display the advanced
settings you can use to control column widths, line styles, and cell gutter
settings as shown in